题目内容
6.根据下列二次函数的图象,写出相应的函数表达式.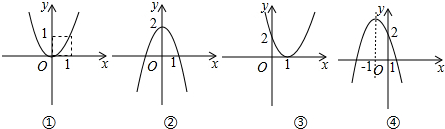
分析 ①②③可根据抛物线顶点坐标设其顶点式,将另一已知点坐标代入求解可得;
④根据抛物线对称轴及其与x轴的一交点求得另一交点,再设其交点式,待定系数求解可得.
解答 解:①由图可知抛物线顶点坐标为(0,0),
可设抛物线解析式为:y=ax2,
将点(1,1)代入,得:a=1,
故抛物线解析式为:y=x2;
②由图可知抛物线顶点坐标为(0,2),
可设抛物线解析式为:y=ax2+2,
将点(1,0)代入,得:a+2=0,
解得:a=-2,
故抛物线解析式为:y=-2x2+2;
③由图可知抛物线顶点坐标为(1,0),
可设抛物线解析式为:y=a(x-1)2,
将点(0,2)代入,得:a=2,
故抛物线解析式为:y=2(x-1)2;
④由图可知抛物线的对称轴为直线x=-1,且抛物线与x轴的一个交点为(1,0),
∴抛物线与x轴的另一交点为(-3,0),
可设抛物线解析式为:y=a(x+3)(x-1),
将点(0,2)代入得:-3a=2,
解得:a=-$\frac{2}{3}$,
故抛物线解析式为:y=-$\frac{2}{3}$(x+3)(x-1)=-$\frac{2}{3}$x2-$\frac{4}{3}$x+2.
点评 本题主要考查待定系数法求二次函数解析式能力,根据不同的已知条件设出合适的解析式是待定系数求解的关键.

练习册系列答案
相关题目
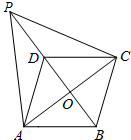 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
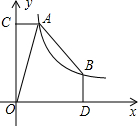 在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.
在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.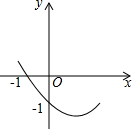 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$. 如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.