题目内容
15.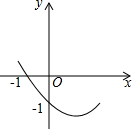 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
分析 由二次函数y=ax2+bx+c的图象过(-1,0)和(0,-1)两点,求c的值及a、b的关系式,根据对称轴的位置判断a的取值范围,再把二次根式化简求值.
解答 解:把(-1,0)和(0,-1)两点代入y=ax2+bx+c中,得
a-b+c=0,c=-1,
∴b=a+c=a-1,
由图象可知,抛物线对称轴x=-$\frac{a-1}{2a}$>0,且a>0,
∴a-1<0,0<a<1,
$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$
=$\sqrt{(a+\frac{1}{a})^{2}}$+$\sqrt{(a-\frac{1}{a})^{2}}$
=|a+$\frac{1}{a}$|+|a-$\frac{1}{a}$|,
=a+$\frac{1}{a}$-a+$\frac{1}{a}$,
=$\frac{2}{a}$.
故答案为:$\frac{2}{a}$.
点评 本题考查了二次函数图象上的点与二次函数解析式的关系,对称轴的性质,根据对称轴的位置确定a的取值范围的解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20.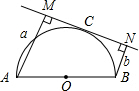 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
5.有理数-2016的相反数是( )
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
 如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.
如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.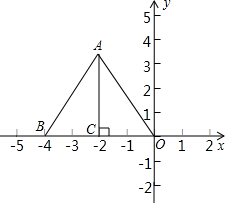 如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.
如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.