题目内容
16. 如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.(1)求∠AOC的度数;
(2)判断OD与AB的位置关系,并说明理由.
分析 (1)根据邻补角的定义列式即可求出∠AOC;
(2)根据角平分线定义求出∠AOD=90°,再根据垂直定义解答.
解答 解:(1)∵∠BOC=3∠AOC,
∠AOC+∠BOC=180°,
∴∠AOC+3∠AOC=180°,
解得∠AOC=45°;
(2)OD⊥AB.理由如下:
∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×45°=90°,
∴OD⊥AB.
点评 本题考查了垂线的定义,邻补角的定义,角平分线的定义,是基础题,根据邻补角的定义列式求出∠AOC是解题的关键.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | x6÷x3=x2 | B. | x2+x2=x4 | C. | 3a-a=2a | D. | x2+x2=x6 |
5.有理数-2016的相反数是( )
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
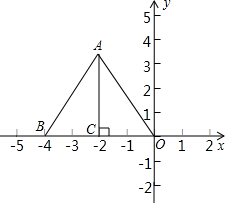 如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.
如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.