题目内容
9.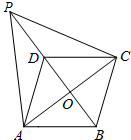 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.(1)求证:PA=PC;
(2)如果PC⊥BC,求证:∠APC=∠BCD.
分析 (1)根据菱形的性质和全等三角形的判定和性质证明即可;
(2)根据菱形的性质和互余进行证明即可.
解答 证明:(1)∵菱形ABCD,
∴AO=OC,OP⊥AC,
∴∠POA=∠POC=90°,
在△PAO与△PCO中$\left\{\begin{array}{l}{AO=OC}\\{∠POA=∠POC}\\{OP=OP}\end{array}\right.$,
∴△PAO≌△PCO(SAS),
∴PA=PC;
(2)∵PC⊥BC,
∴∠CPD+∠PBC=90°,
∴∠APC+∠ABC=180°,
∵∠ABC+∠DCB=180°,
∴∠APC=∠DCB.
点评 本题考查了菱形的性质,关键是根据全等三角形的判定和性质证明.

练习册系列答案
相关题目
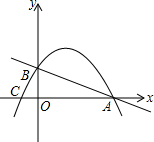 如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).
如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).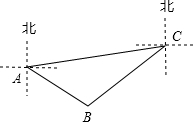 如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)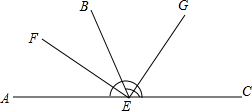 如图,A、E、C在同一直线上,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.
如图,A、E、C在同一直线上,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.