题目内容
11.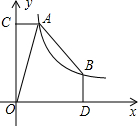 在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.
在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.(1)若k1=2,则AO的长为$\sqrt{5}$,△BOD的面积为1;
(2)若点B的横坐标为k1,且k1>1,当AO=AB时,求k1的值.
分析 (1)由点A的横坐标结合反比例函数的解析式可找出点A的坐标,从而得出AO的长度;再根据反比例函数系数k的几何意义可直接得出S△BOD=$\frac{1}{2}$|k1|,代入k1值即可得出结论;
(2)将A、B点的横坐标代入反比例函数解析式中,可求出点A、B的坐标,结合两点间的距离公式以及AO=AB,即可得出关于k1的一元二次方程,解方程即可得出结论.
解答 解:(1)当k1=2,AC=1时,OC=k1=2,
∴AO=$\sqrt{A{C}^{2}+O{C}^{2}}$=$\sqrt{5}$;
∵k1=2,且S△BOD=$\frac{1}{2}$|k1|=$\frac{1}{2}$×2=1.
故答案为:$\sqrt{2}$;1.
(2)∵AC=1,且点A在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,
∴A点的坐标为(1,k1),
∴AO=$\sqrt{(1-0)^{2}+({k}_{1}-0)^{2}}$=$\sqrt{1+{{k}_{1}}^{2}}$.
∵若点B的横坐标为k1,且点B在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,
∴B点的坐标为(k1,1),
∴AB=$\sqrt{({k}_{1}-1)^{2}+(1-{k}_{1})^{2}}$=$\sqrt{2}$|k1-1|.
又∵AO=AB,即$\sqrt{1+{{k}_{1}}^{2}}$=$\sqrt{2}$|k1-1|,
解得:k1=2-$\sqrt{3}$,或k1=2+$\sqrt{3}$.
点评 本题考查了反比例函数系数k的几何意义以及两点间的距离公式,解题的关键是:(1)根据反比例函数系数k的几何意义直接求面积;(2)由两点间的距离公式得出关于k1的方程.本题属于基础题,难度不大,解决该题型题目时,将点的横坐标代入函数解析式求出点的坐标后,再依据两点间的距离公式以及等量关系找出关于反比例系数k的方程,解方程即可.

 如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )
如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )| A. | 从30°到60°变动 | B. | 从60°到90°变动 | C. | 保持30°不变 | D. | 保持60°不变 |
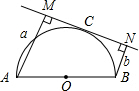 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
| A. | x6÷x3=x2 | B. | x2+x2=x4 | C. | 3a-a=2a | D. | x2+x2=x6 |
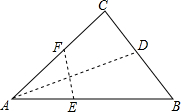 如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.
 已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.
已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$. 如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.
如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.