题目内容
14.先化简,再求值:$\frac{{a}^{2}-4a+4}{{a}^{2}-4}$÷$\frac{a-2}{{a}^{2}+2a}$-3,其中a=$\frac{7}{2}$.分析 根据分式的除法和减法可以化简题目中的式子,然后将a的值代入即可解答本题.
解答 解:$\frac{{a}^{2}-4a+4}{{a}^{2}-4}$÷$\frac{a-2}{{a}^{2}+2a}$-3
=$\frac{(a-2)^{2}}{(a+2)(a-2)}•\frac{a(a+2)}{a-2}-3$
=a-3,
当a=$\frac{7}{2}$时,原式=$\frac{7}{2}-3=\frac{1}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
9.某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是( )
| A. | $\frac{240}{x-20}$-$\frac{120}{x}$=4 | B. | $\frac{240}{x+20}$-$\frac{120}{x}$=4 | C. | $\frac{120}{x}$-$\frac{240}{x-20}$=4 | D. | $\frac{120}{x}$-$\frac{240}{x+20}$=4 |
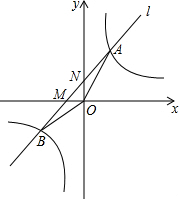 如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).
如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).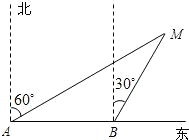 如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?
如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?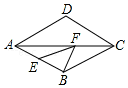 如图,在边长为10的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为5$\sqrt{3}$.
如图,在边长为10的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为5$\sqrt{3}$.