题目内容
8.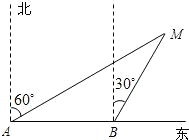 如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?
如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?
分析 根据特殊角的三角函数可以求得MC和BC的长,然后根据勾股定理即可求得BM的长.
解答  解:作MC⊥AB交AB延长线于点C,
解:作MC⊥AB交AB延长线于点C,
由题意可得,
∠MAC=30°,∠MBC=60°,AB=20×0.5=10,
∵$tan∠MAC=\frac{MC}{AC}$,$tan∠MBC=\frac{MC}{BC}$,
∴$\frac{\sqrt{3}}{3}=\frac{MC}{AB+BC}=\frac{MC}{10+BC}$,$\sqrt{3}=\frac{MC}{BC}$,
解得,BC=5,MC=5$\sqrt{3}$,
∴BM=$\sqrt{B{C}^{2}+M{C}^{2}}=\sqrt{{5}^{2}+(5\sqrt{3})^{2}}$=10,
即B处与灯塔M的距离是10海里.
点评 本题考查解直角三角形的应用-方向角问题、勾股定理的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用解直角三角形的相关知识解答.

练习册系列答案
相关题目
17.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{19}}$的值为( )
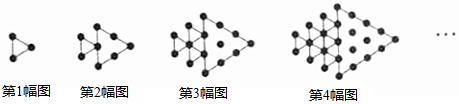

| A. | $\frac{20}{21}$ | B. | $\frac{61}{84}$ | C. | $\frac{589}{840}$ | D. | $\frac{431}{760}$ |
20. 一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
 一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )| A. | 70° | B. | 90° | C. | 110° | D. | 180° |
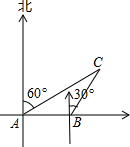 如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.
如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.

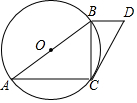 如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.
如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.