题目内容
4．先化简，再求值：$\frac{{x}^{2}-2x}{x}÷（x-\frac{4}{x}）$，其中x=$\sqrt{3}$．分析 先将原式化简，然后将x的值代入即可求出答案．
解答 解：原式=$\frac{x（x-2）}{x}$÷（x-$\frac{4}{x}$）
=（x-2）×$\frac{x}{（x-2）（x+2）}$
=$\frac{x}{x+2}$
当x=$\sqrt{3}$时，
∴原式=$\frac{\sqrt{3}}{2+\sqrt{3}}$=2$\sqrt{3}$-3
点评 本题考查分式的化简求值，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
练习册系列答案
相关题目
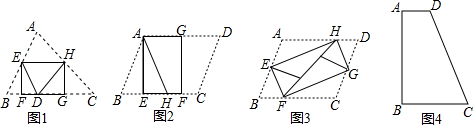
15．
如图，某同学家在A处，现在该同学要去位于B处的同学家去玩，请帮助他选择一条最近的路线（ ）
如图，某同学家在A处，现在该同学要去位于B处的同学家去玩，请帮助他选择一条最近的路线（ ）| A． | A→C→D→B | B． | A→C→F→B | C． | A→C→E→F→B | D． | A→C→M→B |
如图所示是8个完全相同的小正方体组成的几何体，则该几何体的左视图是（ ）
19．
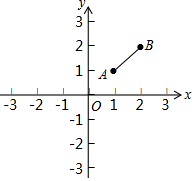如图，在平面直角坐标系xOy中，A（1，1），B（2，2），双曲线y=$\frac{k}{x}$与线段AB有公共点，则k的取值范围是（ ）
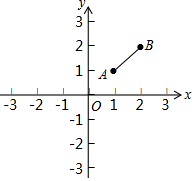如图，在平面直角坐标系xOy中，A（1，1），B（2，2），双曲线y=$\frac{k}{x}$与线段AB有公共点，则k的取值范围是（ ）| A． | k＞0 | B． | k≥1 | C． | k≥4 | D． | 1≤k≤4 |
