��Ŀ����
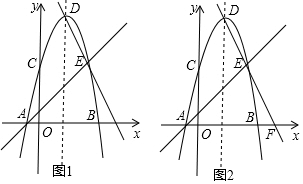
6����ͼ��1����֪��A��2$\sqrt{3}$��2$\sqrt{3}$��������A��x��Ĵ��߽�ֱ��y=-x�ڵ�C������P��ֱ��y=-x�ϵ�һ�����㣬��APB=30�㣬BA��PA����1������P���O�غ�ʱ����ͼ��2����ʾ����ֱ��AB�ĺ�������ʽ��
��2���ڵ�P���˶������У���BҲ��֮�˶������߶�OB����Сֵ��
��3����Q������ƽ���ڵ�����һ�㣬��̽�����Ƿ���������ĵ�Q��ʹ���Ե�B����P����C����QΪ������ı���ʱһ�����Σ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
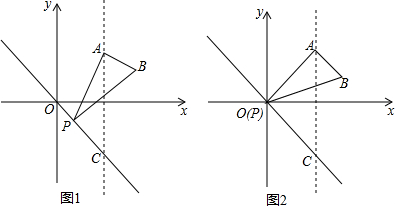
���� ��1����ͼ2�У��ӳ�AB��x���ڵ�D����ֱ�������Σ����D�����꣬���ô���ϵ�������ɽ�����⣻
��2����ͼ1�У���BH��OP��H��ȡPB���е�F������AF��FH��OA��AH������֤����B������HB���˶����Ƴ���OB��BHʱ��OB��ֵ��С����СֵΪOH�ij���
��3�����ڣ���ͼ3�У�����P��H�غ�ʱ����B����P����C����QΪ������ı�����һ�����Σ���ֱ�������Σ����PB�ij��������B���꣬�����е����깫ʽ���ɽ�����⣻
��� �⣺��1����ͼ2�У��ӳ�AB��x���ڵ�D��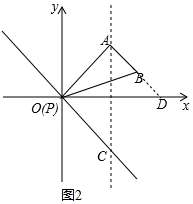
�ߵ�A��2$\sqrt{3}$��2$\sqrt{3}$����BA��PA��
���AOD=45�㣬��OAD=90�㣬
���OADΪ����ֱ�������Σ�
��OD=2��2$\sqrt{3}$=4$\sqrt{3}$��
���D��������4$\sqrt{3}$��0����
��ֱ��AB�ĺ�������ʽΪy=kx+b��k��0����
��A��2$\sqrt{3}$��2$\sqrt{3}$����D��4$\sqrt{3}$��0������y=kx+b��
$\left\{\begin{array}{l}{2\sqrt{3}k+b=2\sqrt{3}}\\{4\sqrt{3}k+b=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-1}\\{b=4\sqrt{3}}\end{array}\right.$��
��ֱ��AB�ĺ�������ʽΪy=-x+4$\sqrt{3}$��
��2����ͼ1�У���BH��OP��H��ȡPB���е�F������AF��FH��OA��AH��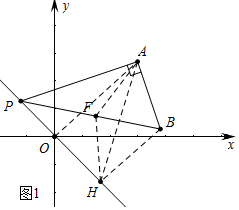
��Rt��PAB��Rt��PBH����PF=FB��
��AF=PF=FB=FH��
��A��P��H��B�ĵ㹲Բ��
���AHB=��APB=30�㣬��AHP=60�㣬
���B������HB���˶���
�൱OB��BHʱ��OB��ֵ��С����СֵΪOH�ij���
��Rt��AOH�У���OA=2$\sqrt{6}$����AHO=60�㣬
��OH=2$\sqrt{2}$��
��OB����СֵΪ2$\sqrt{2}$��
��3�����ڣ�
���ɣ���ͼ3�У�����P��H�غ�ʱ����B����P����C����QΪ������ı�����һ�����Σ�
�ɣ�2����֪H��2��-2�������ı���PBQC�Ǿ��Σ�
��A��2$\sqrt{3}$��2$\sqrt{3}$����
��PA=$\sqrt{��2\sqrt{3}-2��^{2}+��2\sqrt{3}+2��^{2}}$=4$\sqrt{2}$��
��PB=$\frac{PA}{cos30��}$=$\frac{8\sqrt{6}}{3}$��
��B��2+$\frac{8\sqrt{3}}{3}$��$\frac{8\sqrt{3}}{3}$-2����
��BC��PQ�Ľ���D������Ϊ��1+$\frac{7\sqrt{3}}{3}$��$\frac{\sqrt{3}}{3}$-1����
��Q��m��n��������$\frac{m+2}{2}$=1+$\frac{7\sqrt{3}}{3}$��$\frac{n-2}{2}$=$\frac{\sqrt{3}}{3}$-1��
��m=$\frac{14\sqrt{3}}{3}$��n=$\frac{2\sqrt{3}}{3}$��
��Q��$\frac{14\sqrt{3}}{3}$��$\frac{2\sqrt{3}}{3}$����
���� ���⿼��һ�κ����ۺ��⡢��ֱ�������Ρ�����ϵ�������е����깫ʽ��������Ǻ������ĵ㹲Բ�����߶���̵�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ô��߶���̽����ֵ���⣬�����п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ���漸���������ͼ�ǣ�������
���漸���������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
 ��������ͼ��ȷ���ǣ�������
��������ͼ��ȷ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
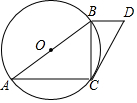 ��ͼ���ڡ�O�У�AB��ֱ������C��Բ�ϣ���A=30�㣬BD��AC����BD=$\frac{1}{3}$AC��
��ͼ���ڡ�O�У�AB��ֱ������C��Բ�ϣ���A=30�㣬BD��AC����BD=$\frac{1}{3}$AC��