题目内容
2.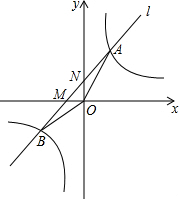 如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).
如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若该反比例函数与过点M(-2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为$\frac{16}{3}$时,求直线l的解析式.
分析 (1)由题意可得A(1,2),利用待定系数法即可解决问题;
(2)把M(-2,0)代入y=kx+b,可得b=2k,可得y=kx+2k,由$\left\{\begin{array}{l}{y=\frac{3k}{x}}\\{y=kx+2k}\end{array}\right.$消去y得到x2+2x-3=0,解得x=-3或1,推出B(-3,-k),A(1,3k),根据△ABO的面积为$\frac{16}{3}$,可得$\frac{1}{2}$•2•3k+$\frac{1}{2}$•2•k=$\frac{16}{3}$,解方程即可解决问题;
解答 解:(1)由题意A(1,2),
把A(1,2)代入y=$\frac{3k}{x}$,得到3k=2,
∴k=$\frac{2}{3}$.
(2)把M(-2,0)代入y=kx+b,可得b=2k,
∴y=kx+2k,
由$\left\{\begin{array}{l}{y=\frac{3k}{x}}\\{y=kx+2k}\end{array}\right.$消去y得到x2+2x-3=0,解得x=-3或1,
∴B(-3,-k),A(1,3k),
∵△ABO的面积为$\frac{16}{3}$,
∴$\frac{1}{2}$•2•3k+$\frac{1}{2}$•2•k=$\frac{16}{3}$,
解得k=$\frac{4}{3}$,
∴直线l的解析式为y=$\frac{4}{3}$x+$\frac{8}{3}$.
点评 本题考查一次函数与反比例函数图象的交点、待定系数法、二元一次方程组等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
10.下列图案中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{19}}$的值为( )
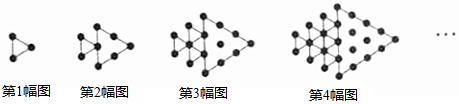

| A. | $\frac{20}{21}$ | B. | $\frac{61}{84}$ | C. | $\frac{589}{840}$ | D. | $\frac{431}{760}$ |
7.某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是( )
| 尺码 | 39 | 40 | 41 | 42 | 43 |
| 平均每天销售数量/件 | 10 | 12 | 20 | 12 | 12 |
| A. | 平均数 | B. | 方差 | C. | 众数 | D. | 中位数 |
 如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )
如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )