题目内容
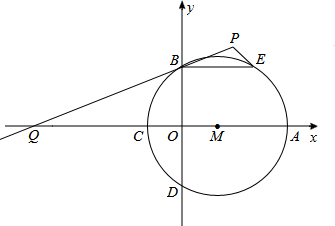 直线y=-
直线y=-
| ||
| 3 |
| 3 |
考点:圆的综合题,全等三角形的判定与性质,等边三角形的判定与性质,特殊角的三角函数值
专题:探究型
分析:延长PB至F,使得PF=PM,连接MF、MB、ME.只需证到BF=PE,只需证到△MBF≌△MEP,只需证到△PFM和△EMB都是等边三角形即可.
解答:解:PB+PE=PM.
理由如下:
延长PB至F,使得PF=PM,连接MF、MB、ME,如图.
∵∠1=60°,PF=PM,
∴△PFM是等边三角形,
∴MF=PM,∠PMF=60°,
∴∠3+∠5=60°.
由直线AB的解析式y=-
x+
可得:A(3,0),B(0,
),
在Rt△AOB中,
∵OB=
,OA=3,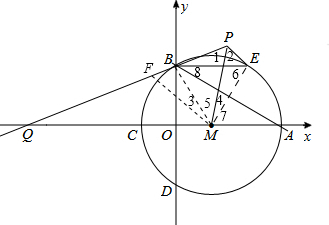
∴tan∠BAO=
,
∴∠BAO=30°.
∵BE∥x轴,
∴∠8=∠BAO=30°,
∴∠7=2∠8=60°.
∵MB=ME,
∴△MBE是等边三角形,∠5+∠4=60°.
∵∠3+∠5=60°,∴∠3=∠4.
在△MBF和△MEP中,
.
∴△MBF≌△MEP(SAS).
∴BF=PE.
∴PM=PF=PB+BF=PB+PE,
即PB+PE=PM.
理由如下:
延长PB至F,使得PF=PM,连接MF、MB、ME,如图.
∵∠1=60°,PF=PM,
∴△PFM是等边三角形,
∴MF=PM,∠PMF=60°,
∴∠3+∠5=60°.
由直线AB的解析式y=-
| ||
| 3 |
| 3 |
| 3 |
在Rt△AOB中,
∵OB=
| 3 |

∴tan∠BAO=
| ||
| 3 |
∴∠BAO=30°.
∵BE∥x轴,
∴∠8=∠BAO=30°,
∴∠7=2∠8=60°.
∵MB=ME,
∴△MBE是等边三角形,∠5+∠4=60°.
∵∠3+∠5=60°,∴∠3=∠4.
在△MBF和△MEP中,
|
∴△MBF≌△MEP(SAS).
∴BF=PE.
∴PM=PF=PB+BF=PB+PE,
即PB+PE=PM.
点评:本题主要考查了圆周角定理、等边三角形的判定与性质、全等三角形的判定与性质、特殊角的三角函数值、平行线的性质等知识,有一定的难度,而用截长补短法构造全等三角形是解决本题的关键,截长补短法是证明一条线段等于两条线段的和(或差)常用的证明方法,应掌握它.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
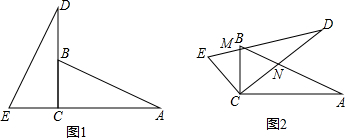
 如图,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
如图,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
 如图,△ABC和△BDE均为等腰直角三角形,AD∥BC,DF=
如图,△ABC和△BDE均为等腰直角三角形,AD∥BC,DF=