题目内容
将连续的偶数2,4,6,8,…,排成如表,请你解答问题.

(1)十字框中的五个数的和与中间的数字18有什么关系?
(2)设中间的数为x用式子表示十字框中的五个数的和.
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和可以分别等于2005和2010吗?如能,求出这五个数;如不能,说明理由.

(1)十字框中的五个数的和与中间的数字18有什么关系?
(2)设中间的数为x用式子表示十字框中的五个数的和.
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和可以分别等于2005和2010吗?如能,求出这五个数;如不能,说明理由.
考点:一元一次方程的应用
专题:
分析:(1)算出这5个数的和,和18进行比较;
(2)由图易知同一竖列相邻的两个数相隔10,横行相邻的两个数相隔2.用中间的数表示出其他四个数,然后相加即可;
(3)求出(2)中的代数式的和等于5x,可列方程求出中间的数,然后根据方程的解的情况就可以作出判断.
(2)由图易知同一竖列相邻的两个数相隔10,横行相邻的两个数相隔2.用中间的数表示出其他四个数,然后相加即可;
(3)求出(2)中的代数式的和等于5x,可列方程求出中间的数,然后根据方程的解的情况就可以作出判断.
解答:解:①8+16+18+20+28=18×5,
故十字框中的五个数的和=中间的数18的5倍;
②设中间的数为x,则十字框的五个数字之和为:
x-10+x-2+x+x+2+x+10=5x,
故5个数字之和为5x;
③不能.
5x=2005,
解得x=401.
而x的个位不能为1,
故十字框框住的5个数字之和不能等于2005;
5x=2010,
解得x=402.
而402不能成为十字框中的5个数的中间的数,
所以字框中的五个数之和可能等于2010.
故十字框中的五个数的和=中间的数18的5倍;
②设中间的数为x,则十字框的五个数字之和为:
x-10+x-2+x+x+2+x+10=5x,
故5个数字之和为5x;
③不能.
5x=2005,
解得x=401.
而x的个位不能为1,
故十字框框住的5个数字之和不能等于2005;
5x=2010,
解得x=402.
而402不能成为十字框中的5个数的中间的数,
所以字框中的五个数之和可能等于2010.
点评:本题考查了一元一次方程的应用.此题注意结合数的排列规律发现左右和上下相邻两个数之间的大小关系,从而完成解答.

练习册系列答案
相关题目
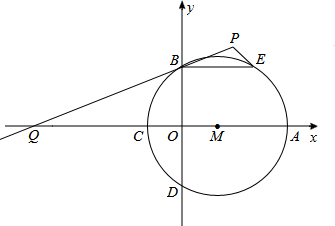 直线y=-
直线y=-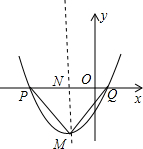 如图,已知二次函数y=x2-(m-3)x-m的图象是抛物线.
如图,已知二次函数y=x2-(m-3)x-m的图象是抛物线.