题目内容
将两块全等的直角三角形如图1摆放,其中∠DCE=∠ACB=90°,∠D=∠A.
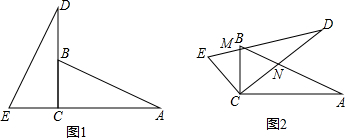
(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图2,AB、CD交于点N,DE、BC交于M,求证:CM=CN.

(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图2,AB、CD交于点N,DE、BC交于M,求证:CM=CN.
考点:全等三角形的判定与性质
专题:
分析:(1)根据直角三角形的性质,可得∠A+∠ABC=90°,根据余角的性质,可得∴∠D+∠ABC=90°,∠D+∠DBF=90°,根据直角三角形的判定,可得答案吧;
(2)根据ASA,可得△ECM和△BCN,根据全等三角形的性质,可得答案.
(2)根据ASA,可得△ECM和△BCN,根据全等三角形的性质,可得答案.
解答:(1)证明:如图延长AB交DE于点F,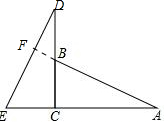 ,
,
∵∠A=∠D,∠DCE=∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠D+∠ABC=90°.
∵∠ABC=∠DBF,
∴∠D+∠DBF=90°,
∴∠DFB=90°,
∴AB⊥DE;
(2)证明:∵∠ECM=45°,∠ECD=90°,
∴∠ECB=∠BCN=45°,
在△ECM和△BCN中,
,
∴△ECM≌△BCNN(ASA),
∴CM=CN.
 ,
,∵∠A=∠D,∠DCE=∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠D+∠ABC=90°.
∵∠ABC=∠DBF,
∴∠D+∠DBF=90°,
∴∠DFB=90°,
∴AB⊥DE;
(2)证明:∵∠ECM=45°,∠ECD=90°,
∴∠ECB=∠BCN=45°,
在△ECM和△BCN中,
|
∴△ECM≌△BCNN(ASA),
∴CM=CN.
点评:本题考查了全等三角形的判定与性质,利用了余角的性质,直角三角形的判定,全等三角形的判定与性质.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
一元二次方程x2-3x-9=0根的情况是( )
| A、有两个相等实数根 |
| B、没有实数根 |
| C、有两个不相等实数根 |
| D、无法确定 |

 如图,在扇形OAB中,⊙O1分别与
如图,在扇形OAB中,⊙O1分别与
 直线y=-
直线y=-