题目内容
 如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.(1)求证:
 |
| EC |
 |
| EA |
(2)若圆的半径为R,求EF的长.
考点:垂径定理,含30度角的直角三角形,勾股定理,圆心角、弧、弦的关系
专题:
分析:(1)首先连接OE,由半径OC⊥AB,EF∥AB,可得OC⊥EF,又由弦EF经过CO的中点D,可求得∠OED的度数,继而可求得∠COE=2∠AOE,继而证得结论;
(2)由勾股定理可求得ED的长,然后由垂径定理求得EF的长.
(2)由勾股定理可求得ED的长,然后由垂径定理求得EF的长.
解答: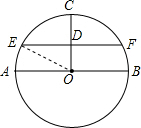 (1)证明:连接OE,
(1)证明:连接OE,
∵D是CO的中点,
∴OD=
OC,
∵径OC⊥AB,EF∥AB,
∴OC⊥EF,
∴∠OED=30°,
∴∠EOC=60°,
∴∠AOE=90°-∠EOC=30°,
∴∠EOC=2∠EOA,
∴
=2
;
(2)解:∵OD=
OE=
R,
∴ED=
=
R,
∴EF=2ED=
R.
 (1)证明:连接OE,
(1)证明:连接OE,∵D是CO的中点,
∴OD=
| 1 |
| 2 |
∵径OC⊥AB,EF∥AB,
∴OC⊥EF,
∴∠OED=30°,
∴∠EOC=60°,
∴∠AOE=90°-∠EOC=30°,
∴∠EOC=2∠EOA,
∴
 |
| EC |
 |
| EA |
(2)解:∵OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴ED=
| OE2-OD2 |
| ||
| 2 |
∴EF=2ED=
| 3 |
点评:此题考查了垂径定理、平行线的性质以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
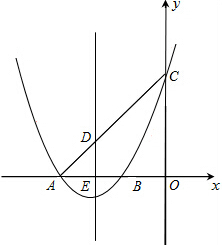 已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.
已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.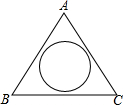 如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.
如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积. 如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则:
如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则: