题目内容
直线L1与L2相交于点A(2,3),L1与x轴交点为M(-1,0),L2与y铀交点为C(0,-2).
(1)求直线L1、L2的函数表达式;
(2)当x取何值时,两个一次函数的值都大于0?
(3)直线L1与x轴交于点M,直线L2与x轴交于点N,求四边形CMAN的面积.
(1)求直线L1、L2的函数表达式;
(2)当x取何值时,两个一次函数的值都大于0?
(3)直线L1与x轴交于点M,直线L2与x轴交于点N,求四边形CMAN的面积.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)利用待定系数法求两个函数解析式;
(2)先确定两直线与x轴的交点坐标,然后根据一次函数的性质,找出两函数图象都在x轴上方所对应的自变量的取值范围;
(3)先确定N点坐标,然后根据三角形面积公式和四边形CMAN的面积=S△AMN+S△CMN进行计算.
(2)先确定两直线与x轴的交点坐标,然后根据一次函数的性质,找出两函数图象都在x轴上方所对应的自变量的取值范围;
(3)先确定N点坐标,然后根据三角形面积公式和四边形CMAN的面积=S△AMN+S△CMN进行计算.
解答:解:(1)设直线L1与的解析式为y=kx+b,
把A(2,3)、M(-1,0)代入得
,
解得
,
所以直线L1与的解析式为y=x+1;
设直线L2的解析式为y=mx+n,
把A(2,3),C(0,-2)代入得
,
解得
,
所以直线L2的解析式为y=
x-2;
(2)当y=0时,
x-2=0,解得x=
,
所以当x>
时,函数y=
x-2的值大于0,
而当x>-1时,函数y=x+1的值大于0,
所以当x>
时,两个一次函数的值都大于0;
(3)由(2)得到N(
,0),
所以四边形CMAN的面积=S△AMN+S△CMN
=
•(
+1)•3+
•(
+1)•2
=
.

把A(2,3)、M(-1,0)代入得
|
解得
|
所以直线L1与的解析式为y=x+1;
设直线L2的解析式为y=mx+n,
把A(2,3),C(0,-2)代入得
|
解得
|
所以直线L2的解析式为y=
| 5 |
| 2 |
(2)当y=0时,
| 5 |
| 2 |
| 4 |
| 5 |
所以当x>
| 4 |
| 5 |
| 5 |
| 2 |
而当x>-1时,函数y=x+1的值大于0,
所以当x>
| 4 |
| 5 |
(3)由(2)得到N(
| 4 |
| 5 |
所以四边形CMAN的面积=S△AMN+S△CMN
=
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
=
| 9 |
| 2 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
甲、乙两地的距离为10km,现在要在甲、乙两地附近建一个商场,则商场与甲、乙两地的距离之和的最小值为( )
| A、5km | B、10km |
| C、15km | D、不能确定 |
 如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
 如图,平面内有4个点A、B、C、D,按下列语句在指定位置上画出图形.
如图,平面内有4个点A、B、C、D,按下列语句在指定位置上画出图形.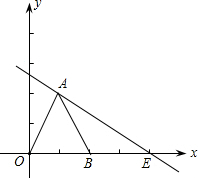 如图,△OAB是边长为2的等边三角形,过点A的直线y=-
如图,△OAB是边长为2的等边三角形,过点A的直线y=-