Question

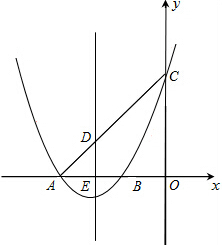已知抛物线y=x²+4x+3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，求抛物线上是否存在点M，使直线CM把四边形DEOC分成面积相等的两部分？若存在，请写出M所在直线的解析式．

Answer 1

考点：二次函数的性质,待定系数法求一次函数解析式

专题：计算题

分析：直线CM交x轴于N，如图，先根据抛物线与x轴的交点问题求出A（-3，0），B（-1，0），则根据对称性得到抛物线的对称轴为直线x=-2，得到E点坐标为（-2，0），接着求出C点坐标为（0，3），再利用待定系数法求出直线AC的解析式为y=x+3，利用直线AC的解析式可确定D点坐标为（-2，1），利用梯形面积公式计算出S_梯形CDEO=4；当直线CM把四边形DEOC分成面积相等的两部分时，S_△OCN=2，根据三角形面积公式得

1

2

•3•ON=2，解得ON=

4

3

，得到N点坐标为（-

4

3

，0），然后利用待定系数法求直线CM的解析式．

解答：解：存在．
直线CM交x轴于N，如图，
当y=0时，x²+4x+3=0，解得x₁=-1，x₂=-3，
则A（-3，0），B（-1，0）；
抛物线的对称轴为直线x=-2，则E点坐标为（-2，0），
当x=0时，y=x²+4x+3=3，则C点坐标为（0，3），
设直线AC的解析式为y=mx+n，
把A（-3，0）、C（0，3）代入得

-3m+n=0 n=3

，解得

m=1 n=3

，则直线AC的解析式为y=x+3，
当x=-2时，y=x+3=1，则D点坐标为（-2，1），
所以S_梯形CDEO=

1

2

×（1+3）×2=4，
因为直线CM把四边形DEOC分成面积相等的两部分，即S_△OCN=2，则

1

2

•3•ON=2，
解得ON=

4

3

，
所以N点坐标为（-

4

3

，0），
设直线CM的解析式为y=kx+b，
把C（0，3），N（-

4

3

，0）代入得

b=3 - 4 3 k+b=0

，
解得

k=- 9 4 b=3

，
所以CM所在直线的解析式为y=-

9

4

x+3．

点评：本题考查了二次函数的性质：二次函数y=ax²+bx+c（a≠0）的顶点坐标是（-

b

2a

，

4ac-b2

4a

），对称轴直线x=-

b

2a

．也考查了抛物线与x轴的交点问题和用待定系数法求一次函数解析式．