题目内容
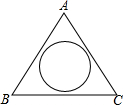 如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.
如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.考点:解直角三角形的应用
专题:
分析:如图,过点A作AD⊥BC于点D,通过解直角△ABD求得AD的长度,则图中空白部分的面积=三角形的面积-圆的面积即可.
解答: 解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.
∵在Rt△ABD中,AB=12米,∠ABC=52°,
∴AD=AB•sin52°≈12×0.788=9.46(米).
∴余下空地的面积=
BC•AD-π×32=
×14×9.46-9π=66.22-9π(米2).
答:余下空地的面积是(66.22-9π)米2.
 解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.∵在Rt△ABD中,AB=12米,∠ABC=52°,
∴AD=AB•sin52°≈12×0.788=9.46(米).
∴余下空地的面积=
| 1 |
| 2 |
| 1 |
| 2 |
答:余下空地的面积是(66.22-9π)米2.
点评:本题考查了解直角三角形的应用.根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
据第六次全国人口普查公布的数据,广东省常住人口约为104300000人,位居全国之首,将104300000用科学记数法表示为( )
| A、0.1043×109 |
| B、10.43×107 |
| C、1.043×109 |
| D、1.043×108 |
有一密码箱的密码有5位数字,若忘记了其中第一位和最后一位,那么一次把它打开的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
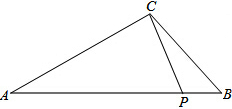 如图,在△ABC中,∠A=30°,∠B=45°,AC=8,点P在线段AB上,连接CP,且tan∠APC=
如图,在△ABC中,∠A=30°,∠B=45°,AC=8,点P在线段AB上,连接CP,且tan∠APC= 如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为
如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为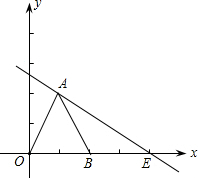 如图,△OAB是边长为2的等边三角形,过点A的直线y=-
如图,△OAB是边长为2的等边三角形,过点A的直线y=-