题目内容
4．若点O是△ABC三边垂直平分线的交点，则有（ ）| A． | OA=OB≠OC | B． | OB=OC≠OA | C． | OC=OA≠OB | D． | OA=OB=OC |
分析 根据线段的垂直平分线的性质判断即可．
解答 解：∵点O是△ABC三边垂直平分线的交点，
∴OA=OB，OA=OC，
∴OA=OB=OC，
故选：D．
点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
14．已知，在四边形ABCD中，∠A=∠B=90°，要使四边形ABCD为矩形，那么需要添加的一个条件是（ ）
| A． | AB=BC | B． | AD=BC | C． | AD=AB | D． | BC=CD |
15．按要求完成下列问题：
（1）若A、B、C、D、E是平面内不同的5个点，则过这5个点的直线可能有多少条？要求确定出可能的条数，并画出每种情况的一种简图；
（2）平面内有n（n为不小于2的整数）个点，过这n个点最多能作多少条直线？完成下列表格．
（1）若A、B、C、D、E是平面内不同的5个点，则过这5个点的直线可能有多少条？要求确定出可能的条数，并画出每种情况的一种简图；
（2）平面内有n（n为不小于2的整数）个点，过这n个点最多能作多少条直线？完成下列表格．
| 点的个数 | 2 | 3 | 4 | 5 | … | 2016 | … | n |
| 能做直线最多条数 | 1 | 3 | 6 | / | … | 2031120 | … | $\frac{n（n-1）}{2}$ |
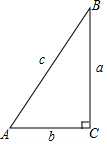如图，在Rt△ABC中，∠C=90°，若a=4，c=5，则tanA=$\frac{4}{3}$．
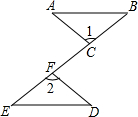如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你再补充一个条件，使△ABC≌△DEF，你补充的条件是FD=AC（答案不唯一）．
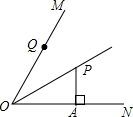如图，OP平分∠MON，PA⊥ON，垂足为A，OA=8，PA=6，Q是射线OM上的一个动点，则线段PQ的最小值是（ ）
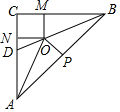如图，已知在△ABC中，BD是角平分线，∠C=90°，∠ABC=∠BAC，O是边BD上一点，OM⊥BC于点M，ON⊥AC于点N，且OM=ON，过点O作OP⊥AB于点P．
14．一个两位数，十位数字是x，个位数字比十位数字的2倍少3，这个两位数是（ ）
| A． | x（2x-3） | B． | x（2x+3） | C． | 12x-3 | D． | 12x+3 |