题目内容
13.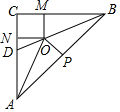 如图,已知在△ABC中,BD是角平分线,∠C=90°,∠ABC=∠BAC,O是边BD上一点,OM⊥BC于点M,ON⊥AC于点N,且OM=ON,过点O作OP⊥AB于点P.
如图,已知在△ABC中,BD是角平分线,∠C=90°,∠ABC=∠BAC,O是边BD上一点,OM⊥BC于点M,ON⊥AC于点N,且OM=ON,过点O作OP⊥AB于点P.(1)求∠ABD的度数;
(2)求证:AO平分∠BAC;
(3)判断BM与AN之间的数量关系,并说明理由.
分析 (1)根据△ABC是等腰直角三角形,BD是角平分线可得∠ABD的度数为22.5°;
(2)根据角平分线的性质定理以及它的逆定理,可得AO平分∠BAC;
(3)根据∠OAP=∠OBP=22.5°,可得AO=BO,再根据HL即可判定Rt△BOM≌Rt△AON,进而得出AN=BM.
解答  解:(1)∵△ABC中,∠C=90°,
解:(1)∵△ABC中,∠C=90°,
∴∠ABC=∠BAC=45°,
又∵BD是角平分线
∴∠ABD的度数为22.5°;
(2)证明:∵OB平分∠CBA,OM⊥BC,OP⊥AB,
∴OM=OP,
∵OM=ON,
∴ON=OP,
又∵ON⊥AC,OP⊥AB,
∴AO平分∠BAC;
(3)BM与AN之间的数量关系:BM=AN.
理由:∵AO平分∠BAC,
∴∠OAP=22.5°,
又∵∠ABD的度数为22.5°,
∴∠OAP=∠OBP,
∴AO=BO,
又∵OM=ON,
∴在Rt△BOM和Rt△AON中,
$\left\{\begin{array}{l}{AO=BO}\\{OM=ON}\end{array}\right.$,
∴Rt△BOM≌Rt△AON(HL),
∴AN=BM.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,角平分线的性质以及三角形内角和定理的综合应用,解决问题的关键是掌握:角的内部到角两边距离相等的点在这个角的平分线上.

练习册系列答案
相关题目
4.若点O是△ABC三边垂直平分线的交点,则有( )
| A. | OA=OB≠OC | B. | OB=OC≠OA | C. | OC=OA≠OB | D. | OA=OB=OC |
8.已知点P在△ABC内,若AP=CP,且AB>BC,则点P一定在( )
| A. | 边AC的垂直平分线上 | B. | 边AB的垂直平分线上 | ||
| C. | 边BC的垂直平分线上 | D. | 边AC的高上 |
18.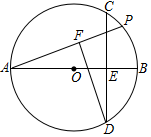 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )| A. | $\frac{\sqrt{3}}{3}$π | B. | $\sqrt{3}$ | C. | $\frac{2}{3}$π | D. | 2 |
3.下面计算正确的是( )
| A. | 3x+2y=6xy | B. | x+x=x2 | C. | 9a2b-9a2b=0 | D. | -9y2+6y2=-3 |
