题目内容
5.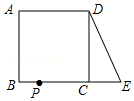 如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.
如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.
分析 分两种情况进行讨论,根据题意得出BP=t-2=1和AP=8-t=1即可求得.
解答 解:因为在△ABP与△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABP=∠DCE}\\{BP=CE}\end{array}\right.$,
∴△ABP≌△DCE,
由题意得:BP=t-2=1,
所以t=3,
因为在△ABP与△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠BAP=∠DCE=90°}\\{AP=CE}\end{array}\right.$,
∴△ABP≌△DCE,
由题意得:AP=8-t=1,
解得t=7.
所以,当t的值为3或7秒时.△ABP和△DCE全等.
故答案为3s或7s
点评 本题考查了全等三角形的判定、正方形的性质,解题的关键是灵活运用所学知识,学会分类讨论,注意不能漏解,属于中考常考题型.

练习册系列答案
相关题目
17.下列算式正确的是( )
| A. | -1-1=0 | B. | 2-2÷(-$\frac{1}{3}$)=0 | C. | |5-2|=-(5-2) | D. | -23=-8 |
14.下列各式计算正确的有( )
| A. | p2•2p3=2p6 | B. | (a+5)2=a2+25 | C. | $\frac{1}{a}+\frac{2}{a}=\frac{3}{a}$ | D. | $\sqrt{9}-\sqrt{4}=\sqrt{5}$ |
 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为m-1=2n.
如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为m-1=2n.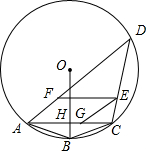 ⊙O是四边形ABCD的外接圆.OB⊥AC.OB与AC相交于点H,BC=2$\sqrt{10}$,AC=CD=12
⊙O是四边形ABCD的外接圆.OB⊥AC.OB与AC相交于点H,BC=2$\sqrt{10}$,AC=CD=12 如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.
如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.