题目内容
16.已知直线y1=x-5与双曲线y2=-$\frac{6-{p}^{2}}{x}$.(1)求证:无论p取何值时,两个函数的图象恒有两个交点;
(2)设两个交点分别为A(x1,y1)、B(x2,y2),且满足x12+x22=3x1x2,求实数p的值.
分析 (1)根据两个函数解析式,得到方程x2-5x+6-p2=0,求根的判别式△,当△>0时,方程总有两个不相等的实数根;
(2)根据根与系的关系求出两根和与两根积,再把x12+x22=3x1x2变形,化成和与乘积的形式,代入计算,得到一个关于p的一元二次方程,解方程即可.
解答 解:(1)联立方程组$\left\{\begin{array}{l}{y=x-5}\\{y=-\frac{6-{p}^{2}}{x}}\end{array}\right.$,可得x2-5x+6-p2=0,
∴△=(-5)2-4×1×(6-p2)=25-24+4p2=1+4p2,
∵无论p取何值时,总有4p2≥0,
∴△=1+4p2>0,
∴无论p取何值时,方程总有两个不相等的实数根;
(2)∵x1+x2=5,x1x2=6-p2,
又∵x12+x22=3x1x2,
∴(x1+x2)2-2x1x2=3x1x2,
∴52=5(6-p2),
解得p=±1,
∴实数p的值为±1.
点评 本题属于一次函数与反比例函数图象的交点问题,主要考查了根的判别式和根与系数的关系的运用,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
6. 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )| A. | △ODB与△OCA的面积相等 | |
| B. | 当点A是PC的中点时,点B一定是PD的中点 | |
| C. | 只有当四边形OCPB为正方形时,四边形PAOB的面积最大 | |
| D. | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
7.菱形的边长为5,一内角为60°,则较长对角线长为( )
| A. | $\frac{5}{2}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 5 | D. | 5$\sqrt{3}$ |
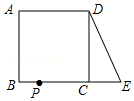 如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.
如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.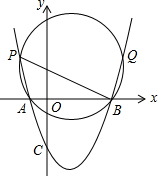 抛物线y=x2-2x-3交x轴于A(-1,0),B(3,0)以AB为弦的圆与抛物线x轴上方部分交于P、Q两点(P左,Q右),且∠APB=45°,求点P,Q的坐标.
抛物线y=x2-2x-3交x轴于A(-1,0),B(3,0)以AB为弦的圆与抛物线x轴上方部分交于P、Q两点(P左,Q右),且∠APB=45°,求点P,Q的坐标.