题目内容
13.阅读下列材料:计算(-$\frac{1}{30}$)÷($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)
解法①:原式=(-$\frac{1}{30}$)÷$\frac{2}{3}$-(-$\frac{1}{30}$)÷$\frac{1}{10}$+(-$\frac{1}{30}$)÷$\frac{1}{6}$-(-$\frac{1}{30}$)÷$\frac{2}{5}$
=-$\frac{1}{20}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{12}$=$\frac{1}{6}$
解法②:原式=(-$\frac{1}{30}$)÷[($\frac{2}{3}$+$\frac{1}{6}$)-($\frac{1}{10}$+$\frac{2}{5}$)]=(-$\frac{1}{30}$)÷($\frac{5}{6}$-$\frac{1}{2}$)=-$\frac{1}{30}$×3=-$\frac{1}{10}$
解法③:原式的倒数为($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)÷(-$\frac{1}{30}$)=($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)×(-30)=-20+3-5+12=-10故原式=-$\frac{1}{10}$
(1)上面得出的结果不同,其中肯定有错误的解法,你认为解法①是错误的.在正确的解法中,你认为解法③最简便,该解法运用的运算律是乘法分配律.
(2)请计算:(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$).
分析 (1)上面得出的结果不同,有错误的解法,我认为解法①是错误的.在正确的解法中,我认为解法③最简便,该解法运用的运算律是乘法分配律.
(2)首先应用乘法分配律,求出(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$)的倒数为多少;然后根据算式的倒数,求出算式(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$)的值是多少即可.
解答 解:(1)上面得出的结果不同,有错误的解法,我认为解法①是错误的.在正确的解法中,我认为解法③最简便,该解法运用的运算律是乘法分配律.
(2)∵($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$)÷(-$\frac{1}{42}$)
=($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$)×(-42)
=$\frac{1}{6}$×(-42)-$\frac{3}{14}$×(-42)+$\frac{2}{3}$×(-42)-$\frac{3}{7}$×(-42)
=-7+9-28+18
=-8
∴(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{3}{7}$)=-$\frac{1}{8}$
故答案为:①、③、乘法分配律.
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法分配律的应用.

 名校课堂系列答案
名校课堂系列答案
| A. | 3n-1 | B. | 3n+1 | C. | 4n-1 | D. | 4n+1 |
| A. | a8÷a4=a2 | B. | 2a2+a=3a3 | C. | (a4)2=a6 | D. | a3•a4=a7 |
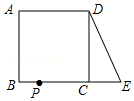 如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.
如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为3s或7s.