题目内容
2.若am=3,an=4,则a2m+3n=576.分析 首先根据幂的乘方的运算方法:(am)n=amn,分别求出a2m、a3n的值各是多少;然后根据同底数幂的乘方法则,求出算式a2m+3n的值是多少即可.
解答 解:∵am=3,an=4,
∴a2m=32=9,a3n=43=64,
∴a2m+3n=a2m•a3n=9×64=576.
故答案为:576.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
相关题目
12.计算:p2•p3=P5;($\frac{1}{2}{a}^{2}b$)3=$\frac{1}{8}$a6b3;(-$\frac{1}{2}$)2015×22014=-$\frac{1}{2}$.
13.如果把分式$\frac{2x}{x-y}$中的x和y都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小$\frac{1}{5}$ |
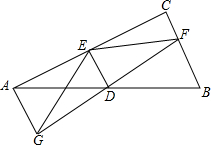 已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA.
已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA. 已知长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与B重合,折痕为EF.
已知长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与B重合,折痕为EF. 如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.
如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.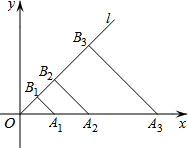 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn-1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是(1,1),B3的坐标是(4,4),Bn的坐标是(2n-1,2n-1).
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn-1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是(1,1),B3的坐标是(4,4),Bn的坐标是(2n-1,2n-1).
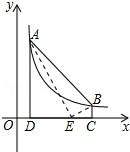 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.