题目内容
 已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.(1)求点A、点B的坐标;
(2)求一次函数的解析式.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)根据解析式即可求得A的坐标,根据OA=2OB求得OB=2,由于一次函数y=kx+4的图象与x轴正半轴的交点为B,所以B的坐标为(-2,0);
(2)将B(2,0)的坐标代入y=kx+4即可求得;
(2)将B(2,0)的坐标代入y=kx+4即可求得;
解答:解:(1)∵一次函数y=kx+4的图象与y轴的交点为A,
∴点A的坐标为A(0,4),
∴OA=4,
∵OA=2OB,
∴OB=2,
∵一次函数y=kx+4的图象与x轴正半轴的交点为B,
∴点B的坐标为B(2,0).
(2)将B(2,0)的坐标代入y=kx+4,得 0=2k+4,
解得 k=-2,
所以一次函数的解析式为 y=-2x+4.
∴点A的坐标为A(0,4),
∴OA=4,
∵OA=2OB,
∴OB=2,
∵一次函数y=kx+4的图象与x轴正半轴的交点为B,
∴点B的坐标为B(2,0).
(2)将B(2,0)的坐标代入y=kx+4,得 0=2k+4,
解得 k=-2,
所以一次函数的解析式为 y=-2x+4.
点评:此题考查点的坐标与解析式的关系以及待定系数法的应用,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
矩形ABCD中,两对角线AC与BD相交于点O,AB=1,∠DBC=30°,则△DOC的周长为( )
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、2+
|
 如图,直线y=kx+b与坐标轴的两交点分别为A(2,0)和B(0,-3),则不等式kx+b+3≤0的解为( )
如图,直线y=kx+b与坐标轴的两交点分别为A(2,0)和B(0,-3),则不等式kx+b+3≤0的解为( )| A、x≤0 | B、x≥0 |
| C、x≥2 | D、x≤2 |

 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.
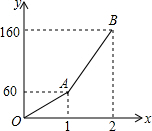 己知:一辆汽车在行驶的过程中,路程y(单位:km)与时间x(单位:h)之间的函数关系如图.
己知:一辆汽车在行驶的过程中,路程y(单位:km)与时间x(单位:h)之间的函数关系如图.