题目内容
根据绝对值的几何意义知:
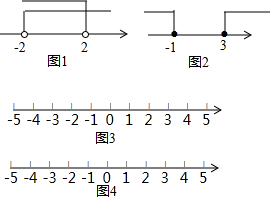
(1)不等式|x|<2的解集就是数轴上离开原点(0)的距离小于2的所有点的集合.在数轴上表示如图1所示,即不等式|x|<2的解集为-2<x<2.
(2)不等式|x-1|>2的解集就是数轴上离开表示1的点的距离大于2的所有点的集合,在数轴上表示如图2所示,即不等式|x-1|>2的解集为x<-1或x>3.
(3)根据(1)、(2)的结论,完成下列解答:
①不等式|x|>2的解集就是数轴上离开 的所有点的集合.请在图3中表示|x|>2的解集,即不等式|x|>2的解集为 .
②不等式|x+1|<3的解集就是数轴上离开 的所有点的集合,请在图4中表示|x+1|<3的解集,即不等式|x+1|<3的解集为 .
解决问题:
根据上面提供的信息,对于绝对值不等式|x-a|<b(b>0)和|x-a|>b(b>0),请直接写出它们的解集分别为 , .
(1)不等式|x|<2的解集就是数轴上离开原点(0)的距离小于2的所有点的集合.在数轴上表示如图1所示,即不等式|x|<2的解集为-2<x<2.
(2)不等式|x-1|>2的解集就是数轴上离开表示1的点的距离大于2的所有点的集合,在数轴上表示如图2所示,即不等式|x-1|>2的解集为x<-1或x>3.
(3)根据(1)、(2)的结论,完成下列解答:
①不等式|x|>2的解集就是数轴上离开
②不等式|x+1|<3的解集就是数轴上离开
解决问题:
根据上面提供的信息,对于绝对值不等式|x-a|<b(b>0)和|x-a|>b(b>0),请直接写出它们的解集分别为

考点:一元一次不等式组的应用,绝对值
专题:
分析:根据绝对值的几何意义进行填空.利用(1)、(2)的材料,结合数轴进行解答.
解答: 解:①不等式|x|>2的解集就是数轴上离开 原点(0)的距离大于2的所有点的集合.如图3所示:不等式|x|>2的解集为 x>2或x<-2.
解:①不等式|x|>2的解集就是数轴上离开 原点(0)的距离大于2的所有点的集合.如图3所示:不等式|x|>2的解集为 x>2或x<-2.
故答案是:x>2或x<-2;
②不等式|x+1|<3的解集就是数轴上离开 表示1的点的距离小于3的所有点的集合,如图4所示:不等式|x+1|<3的解集为-4<x<2.
故答案是:-4<x<2;
解决问题:
不等式|x-a|<b(b>0)和|x-a|>b(b>0),请直接写出它们的解集分别为 a-b<x<a+b,x<a-b或x>a+b.
故答案是:a-b<x<a+b;x<a-b或x>a+b.
 解:①不等式|x|>2的解集就是数轴上离开 原点(0)的距离大于2的所有点的集合.如图3所示:不等式|x|>2的解集为 x>2或x<-2.
解:①不等式|x|>2的解集就是数轴上离开 原点(0)的距离大于2的所有点的集合.如图3所示:不等式|x|>2的解集为 x>2或x<-2.故答案是:x>2或x<-2;
②不等式|x+1|<3的解集就是数轴上离开 表示1的点的距离小于3的所有点的集合,如图4所示:不等式|x+1|<3的解集为-4<x<2.
故答案是:-4<x<2;
解决问题:
不等式|x-a|<b(b>0)和|x-a|>b(b>0),请直接写出它们的解集分别为 a-b<x<a+b,x<a-b或x>a+b.
故答案是:a-b<x<a+b;x<a-b或x>a+b.
点评:本题考查了一元一次不等式组的应用和绝对值.注意数形结合数学思想的应用.

练习册系列答案
相关题目
下列图形经过折叠后,能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
 如图,OB平分∠AOD,∠AOC=45°,∠COD=25°,则∠BOC=( )
如图,OB平分∠AOD,∠AOC=45°,∠COD=25°,则∠BOC=( )| A、5° | B、10° |
| C、15° | D、20° |
 如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0).
如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0). 已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB. 已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.
已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.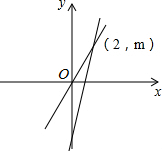 如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点.
如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点. 在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.
在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.