题目内容
矩形ABCD中,两对角线AC与BD相交于点O,AB=1,∠DBC=30°,则△DOC的周长为( )
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、2+
|
考点:矩形的性质
专题:
分析:根据矩形性质求出AO=OD=
BD,根据含30度角的直角三角形性质求出BD,即可求出答案.
| 1 |
| 2 |
解答:解:∵四边形ABCD是矩形,
∴AC=BD,AO=OC,OB=OD,AD∥BC,AB=CD=1,∠DAB=∠DCB=90°,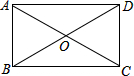
∴AO=OD=
BD,
∵∠DBC=30°,
∴BD=2DC=2,
∴OA=OD=OC=1,
∴△DOC的周长是OC+DC+OD=1+1+1=3,
故选A.
∴AC=BD,AO=OC,OB=OD,AD∥BC,AB=CD=1,∠DAB=∠DCB=90°,

∴AO=OD=
| 1 |
| 2 |
∵∠DBC=30°,
∴BD=2DC=2,
∴OA=OD=OC=1,
∴△DOC的周长是OC+DC+OD=1+1+1=3,
故选A.
点评:本题考查了平行线性质,矩形的性质,勾股定理的应用,注意:矩形的对边平行且相等,矩形的对角线相等且互相平分.

练习册系列答案
相关题目
有铅笔、练习本、圆珠笔三种学习用品,若购铅笔1支,练习本2本共需4元,购1本练习本比1支圆珠笔多花1元,那么购铅笔、练习本、圆珠笔各1件共需( )
| A、3元 | B、2元 |
| C、1元 | D、0.9元 |
如果
是二元一次方程mx+y=3的一个解,则m的值是( )
|
| A、-2 | B、2 | C、-1 | D、1 |
下列图形经过折叠后,能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是
如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是( )
| A、x>5 | B、x<5 |
| C、x>3 | D、x<3. |
已知
是关于x,y的方程x+my=3的一个解,则m的值为( )
|
| A、-1 | B、-2 | C、2 | D、3 |
 如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为
如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 如图是由4个边长为1的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为
如图是由4个边长为1的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为 已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.