题目内容
 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.(1)P点的坐标为(
(2)△MPA面积的有最大值吗,若有请求此时x的值;
(3)探索:当x为何值时,△MPA是一个等腰三角形?请写出你的研究成果.
考点:四边形综合题
专题:
分析:(1)根据PG和OG的长度即可求得P的坐标;
(2)可通过求△MPA的面积和x的函数关系式来得出△MPA的面积最大值及对应的x的值.
(3)△MPA为等腰三角形,则PM=PA或PM=MA或PA=AM即可,分别求x的值,即可解题.
(2)可通过求△MPA的面积和x的函数关系式来得出△MPA的面积最大值及对应的x的值.
(3)△MPA为等腰三角形,则PM=PA或PM=MA或PA=AM即可,分别求x的值,即可解题.
解答:解:(1)动点运动x秒后,则BN=x,
 则PG=
则PG=
x,CN=3-x,
∵∠ACB=∠PCN,∠ABC=∠PNC=90°,
∴△CPN∽△CAB,
∴
=
,又CN=3-x,AB=4,BC=3,
∴PN=
(3-x),
则PG=NG-NP=4-
(3-x)=
x,
∴P点的坐标为 (3-x,
x);
(2)设△MPA的面积为S,在△MPA中,MA=3-x,MA边上的高为
x,
其中,0≤x<3,
∴S=
(3-x)×
x=
(-x2+3x)=-
(x-
)2+
,
∴S的最大值为
,此时x=
;
(3)要使得△MPA为等腰三角形,
①AP=PM,使得AG=MG即可,
MG=3-x-x=3-2x,AG=x,解得x=1,
②AM=AP,则AM=3-x,AP=
x,解得x=
,
③PM=AM,则AM=3-x,PM=
,解得x=
,
故x=1或
或
时,△MPA为等腰三角形.
 则PG=
则PG=| 4 |
| 3 |
∵∠ACB=∠PCN,∠ABC=∠PNC=90°,
∴△CPN∽△CAB,
∴
| PN |
| AB |
| CN |
| CB |
∴PN=
| 4 |
| 3 |
则PG=NG-NP=4-
| 4 |
| 3 |
| 4 |
| 3 |
∴P点的坐标为 (3-x,
| 4 |
| 3 |
(2)设△MPA的面积为S,在△MPA中,MA=3-x,MA边上的高为
| 4 |
| 3 |
其中,0≤x<3,
∴S=
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴S的最大值为
| 3 |
| 2 |
| 3 |
| 2 |
(3)要使得△MPA为等腰三角形,
①AP=PM,使得AG=MG即可,
MG=3-x-x=3-2x,AG=x,解得x=1,
②AM=AP,则AM=3-x,AP=
| 5 |
| 3 |
| 9 |
| 8 |
③PM=AM,则AM=3-x,PM=
(3-2x)2+(
|
| 54 |
| 43 |
故x=1或
| 9 |
| 8 |
| 54 |
| 43 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了相似三角形对应边比值相等的性质,考查了二次函数的应用、矩形的性质、图形面积的求法等知识点,考查学生分类讨论,数形结合的数学思想方法,本题中列出关于x的关系式并求解是解题的关键.

练习册系列答案
相关题目
下面各对数值中,属于方程x2-3y=0的解的一对是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图是由4个边长为1的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为
如图是由4个边长为1的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为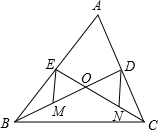 如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点. 已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
已知:在平面直角坐标系xOy中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
 如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB和BC于点F和E.若DB=8,AD=
如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB和BC于点F和E.若DB=8,AD=