题目内容
18.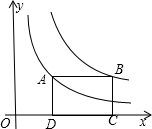 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
分析 根据题意表示出x1=$\frac{{k}_{1}}{a}$,x2=$\frac{{k}_{2}}{a}$,进而求得AB=CD=$\frac{{k}_{2}}{a}$-$\frac{{k}_{1}}{a}$=$\frac{{k}_{2}-{k}_{1}}{a}$,根据矩形ABCD的周长始终保持不变,得出2($\frac{{k}_{2}-{k}_{1}}{a}$+a)=m(m为常数),经过变形得到k2-k1=-a2+$\frac{m}{2}$a,从而得出(k2-k1)的值随a的增大而先增大后减小.
解答 解:∵点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,
∴x1=$\frac{{k}_{1}}{a}$,x2=$\frac{{k}_{2}}{a}$,
∴AB=CD=$\frac{{k}_{2}}{a}$-$\frac{{k}_{1}}{a}$=$\frac{{k}_{2}-{k}_{1}}{a}$,
∵矩形ABCD的周长始终保持不变,
∴设2($\frac{{k}_{2}-{k}_{1}}{a}$+a)=m,
∴k2-k1=-a2+$\frac{m}{2}$a,
∴(k2-k1)是关于a的二次函数,
∵-1<0,
∴(k2-k1)的值随a的增大而先增大后减小.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征以及矩形的周长,图象上的点适合解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列运算正确的是( )
| A. | 2a2+3a2=5a4 | B. | a2•a3=a5 | C. | (3a2)3=9a6 | D. | (a-b)2=a2-b2 |
6.-6的相反数是( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
3.已知关于x的一元二次方程x2-2x+k=0有两个实数根,则k的值是( )
| A. | k<1 | B. | k≤1 | C. | k>-1 | D. | k≤-1 |
 如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.
如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.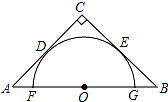 如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=1,则△ABC的周长为8+6$\sqrt{2}$.
如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=1,则△ABC的周长为8+6$\sqrt{2}$.