题目内容
3.已知关于x的一元二次方程x2-2x+k=0有两个实数根,则k的值是( )| A. | k<1 | B. | k≤1 | C. | k>-1 | D. | k≤-1 |
分析 根据判别式的意义得到△=(-2)2-4k≥0,然后解不等式即可.
解答 解:根据题意得△=(-2)2-4k≥0,
解得k≤1.
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
 图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )| A. | 主视图 | B. | 俯视图 | ||
| C. | 左视图 | D. | 主视图、俯视图和左视图都改变 |
14.某市政工程队准备修连一条长1200m的污水处理管道.在修建完400m后,为了能赶在讯期前完成,采用新技术,工效比原来提升了25%.结果比原计划提前4天完成任务.设原计划每天修建管道xm,依题意列方程得( )
| A. | $\frac{1200}{x}-\frac{1200}{x(1+25%)}=4$ | B. | $\frac{1200-400}{x(1+25%)}-\frac{1200-400}{x}=4$ | ||
| C. | $\frac{1200}{x}-\frac{1200-400}{x(1+25%)}=4$ | D. | $\frac{1200-400}{x}-\frac{1200-400}{x(1+25%)}=4$ |
11. 甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是( )
甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是( )
 甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是( )
甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是( )| A. | 甲同学7次测试成绩的众数为20和30,中位数为30 | |
| B. | 乙同学7次测试成绩的中位数为30,7次测试成绩中甲同学成绩较稳定 | |
| C. | 甲同学7次测试成绩的众数为20,中位数为30 | |
| D. | 乙同学7次测试成绩的众数为10和30,7次测试成绩中乙同学成绩较稳定 |
18.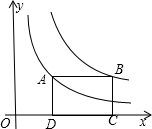 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
12.下列各式的计算过程及结果都正确的是( )
| A. | $\frac{y}{5x}÷\frac{1}{3}x=\frac{y}{5x}•3x=\frac{3}{5}y$ | |
| B. | $8xy÷\frac{4x}{y}=\frac{1}{8xy}•\frac{4x}{y}=\frac{1}{2{y}^{2}}$ | |
| C. | $\frac{x}{2a}÷\frac{2b}{y}=\frac{x}{2a}•\frac{y}{2b}=\frac{xy}{2ab}$ | |
| D. | $\frac{x+y}{{x}^{2}-xy}÷\frac{1}{x-y}=\frac{x+y}{x(x-y)}•(x-y)=\frac{x+y}{x}$ |
13.若代数式$\frac{1}{\sqrt{x+2}}$有意义,则实数x的取值范围是( )
| A. | x≥-2 | B. | x>-2 | C. | x≤-2 | D. | x<-2 |
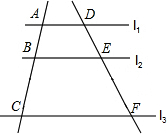 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.