题目内容
8. 如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.
如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.(1)写出与点B有关的三条不同类型的结论.(不另外添加字母或线段)
(2)若AG=3FG,求tanA的值.
分析 (1)由切线的性质和圆的性质即可得出结论;
(2)连接OB,由AG=3FG,推出FG=OG=$\frac{1}{2}$OF,得到OG=$\frac{1}{2}$OB,根据直角三角形的性质得到∠GBO=30°,即可求得∠A=$\frac{1}{2}∠BOG$=30°,于是得到结果.
解答  解:(1)与点B有关的结论:BG⊥AF,BC=CM;
解:(1)与点B有关的结论:BG⊥AF,BC=CM;
(2)如图,连接OB,
∵AG=3FG,
∴FG=OG=$\frac{1}{2}$OF,
∴OG=$\frac{1}{2}$OB,
∵BG⊥AF,
∴∠GBO=30°,
∴∠BOG=60°,∵OB=OA,
∴∠A=$\frac{1}{2}∠BOG$=30°,
∴tan∠A=$\frac{\sqrt{3}}{3}$.
点评 本题考查了切线的性质,直角三角形的性质,锐角三角函数,熟记直角三角形的性质是解题的关键.

练习册系列答案
相关题目
13. 图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
 图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )| A. | 主视图 | B. | 俯视图 | ||
| C. | 左视图 | D. | 主视图、俯视图和左视图都改变 |
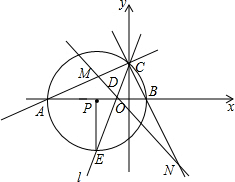 在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.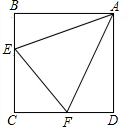 如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.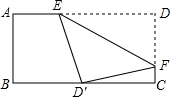 如图,将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合.若BC=6,CD=4,则CF=$\frac{7}{8}$.
如图,将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合.若BC=6,CD=4,则CF=$\frac{7}{8}$.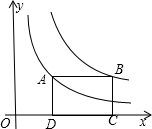 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )