题目内容
10.有一扇形的铁皮,其半径为30cm,圆心角为60°,若用此扇形铁皮围成一个圆锥形的教具(不计接缝),则此圆锥的高是5$\sqrt{35}$cm.分析 根据题目提供的数据求出扇形的弧长,根据扇形的弧长等于圆锥地面的周长求出圆锥的半径,然后在圆锥的高、母线和底面半径构造的直角三角形中求圆锥的高.
解答 解:扇形的弧长为:$\frac{60π×30}{180}$=10π,
∵扇形的弧长等于圆锥的底面周长,
∴2πr=10π,
解得:r=5,
∴圆锥的高为:$\sqrt{3{0}^{2}-{5}^{2}}$=5$\sqrt{35}$cm.
故答案为:5$\sqrt{35}$cm.
点评 本题考查了圆锥的侧面展开图的弧长与圆锥的底面半径之间的转化,解决本题的关键是根据圆锥的侧面弧长转化为圆锥的底面周长,求出半径后,构造直角三角形求圆锥的高.

练习册系列答案
相关题目
18.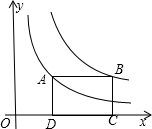 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
5.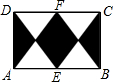 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{17}{38}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
19.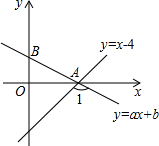 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )| A. | y=-$\frac{1}{2}$x+2 | B. | y=$\frac{1}{2}$x+2 | C. | y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$ |
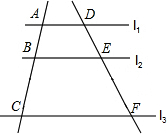 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.