题目内容
13.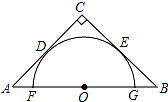 如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=1,则△ABC的周长为8+6$\sqrt{2}$.
如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=1,则△ABC的周长为8+6$\sqrt{2}$.
分析 首先连接OD,OE,易证得四边形ODCE是正方形,△OEB是等腰直角三角形,首先设OE=r,由OB=$\sqrt{2}$OE=$\sqrt{2}$r,可得方程:1+r=$\sqrt{2}$r,解此方程,即可求得答案.
解答  解:连接OD,OE,
解:连接OD,OE,
∵半圆O与等腰直角三角形两腰CA、CB分别切于D、E两点,
∴∠C=∠OEB=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形,
∴CD=CE=OE,
∵∠A=∠B=45°,
∴∠EOB=∠EBO=45°,
∴OE=EB,
∴△OEB是等腰直角三角形,
设OE=r,
∴BE=OE=OG=r,
∴OB=OG+BG=1+r,
∴OB=$\sqrt{2}$OE=$\sqrt{2}$r,
∴1+r=$\sqrt{2}$r,
∴r=$\sqrt{2}$+1,
∴AC=BC=2$\sqrt{2}$+2,
AB=2$\sqrt{2}$($\sqrt{2}+1$)=4+2$\sqrt{2}$,
∴△ABC的周长=8+6$\sqrt{2}$,
故答案为:8+6$\sqrt{2}$.
点评 此题考查了切线的性质、正方形的判定与性质以及等腰直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4. 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
8.从青岛到济南有南线和北线两条高速公路,南线全长400千米,北线全长320千米.甲、乙两辆客车分别有南线和北线从青岛同时驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南.若设客车乙从青岛到济南的平均速度是x千米/小时,则根据题意可得方程( )
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
18.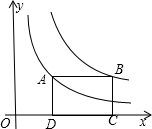 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
5.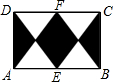 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{17}{38}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
3. 如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
 如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )| A. | 3cm | B. | 2cm | C. | 4cm | D. | $\sqrt{3}$cm |