题目内容
7.若关于x的一元二次方程(m-1)x2+3x-2=0总有两个不相等的实数根,则实数m的取值范围是m>-$\frac{1}{8}$且m≠1.分析 根据一元二次方程的定义以及根的判别式的意义得到△=9-4(m-1)(-2)>0且m-1≠0,求出m的取值范围即可.
解答 解:∵关于x的一元二次方程(m-1)x2+3x-2=0总有两个不相等的实数根,
∴△>0且m-1≠0,
∴9-4(m-1)(-2)>0且m-1≠0,
∴m>-$\frac{1}{8}$且m≠1,
故答案为:m>-$\frac{1}{8}$且m≠1.
点评 本题主要考查了根的判别式以及一元二次方程的意义的知识,解答本题的关键是熟练掌握方程有两个不相等的实数根,则根的判别式△>0,此题难度不大.

练习册系列答案
相关题目
18.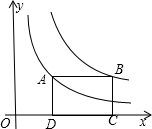 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
12.下列各式的计算过程及结果都正确的是( )
| A. | $\frac{y}{5x}÷\frac{1}{3}x=\frac{y}{5x}•3x=\frac{3}{5}y$ | |
| B. | $8xy÷\frac{4x}{y}=\frac{1}{8xy}•\frac{4x}{y}=\frac{1}{2{y}^{2}}$ | |
| C. | $\frac{x}{2a}÷\frac{2b}{y}=\frac{x}{2a}•\frac{y}{2b}=\frac{xy}{2ab}$ | |
| D. | $\frac{x+y}{{x}^{2}-xy}÷\frac{1}{x-y}=\frac{x+y}{x(x-y)}•(x-y)=\frac{x+y}{x}$ |
19.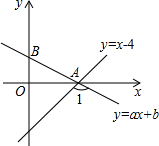 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )| A. | y=-$\frac{1}{2}$x+2 | B. | y=$\frac{1}{2}$x+2 | C. | y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$ |
17.将抛物线y=2(x-1)2+1向右平移1个单位长度,再向下移1个单位长度,所得的抛物线解析式为( )
| A. | y=2x2+1 | B. | y=2(x-2)2+2 | C. | y=2(x-2)2 | D. | y=2x2 |
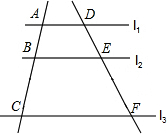 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.