题目内容
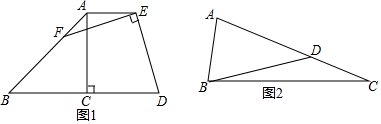
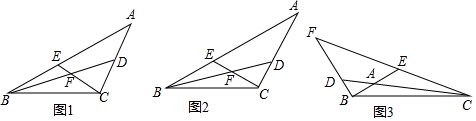
4.在△ABC中,点D、E分别在边AC、AB上,BD、CE交于点F,CE=BE,且∠BEC+∠BDC=180°(1)如图1,当∠BEC=120°时,与AC相等的线段是BF;(请直接写出答案)
(2)如图2,当∠BEC≠120°时,(1)中的结论是否成立,若成立请证明,若不成立,请说明理由;
(3)如图3,点D、E分别在边CA、BA的延长线上时,BD、CE交于点F,若将条件CE=BE改为“CE=kBE”,且BF=m,EF=n,∠BFE=α,其它条件不变,求AE的长(用含k,m,n,α的式子表示)
分析 (1)先判断出∠BEC=∠CGA,BE=CG,进而得出△BEF≌△CGA,即可得出结论;
(2)同(1)的方法直接得出结论;
(3)同(1)的方法得出∠BEC=∠CGA,再用同弧所对的圆周角相等,进而得出△BFG∽△CAE,即可得出AE=kFG,进而用锐角三角函数和等腰三角形的性质得出FG,即可.
解答 解:(1)BF=AC,
理由:如图1, 过点B,C,D作圆交AB于G,连接CG,
过点B,C,D作圆交AB于G,连接CG,
∴∠BGC=∠BDC,
∵∠BEC+∠BDC=180°,
∴∠BEC+∠BGC=180°,
∴∠BGC+∠AGC=180°,
∴∠BEC=∠CGA,
∵∠BEC+∠BDC=180°,∠BEC+∠AEC=180°,
∴∠BDC=∠AEC,
∵∠BDC=∠BGC,
∴∠CEG=∠CGE,
∴CE=CG,
∵CE=BE,
∴BE=CG,
在△BEF和△CGA中,$\left\{\begin{array}{l}{∠BEC=∠CGA}\\{BE=CG}\\{∠EBF=∠GCA(同弧所对的圆周角相等)}\end{array}\right.$,
∴△BEF≌△CGA,
∴BF=AC,
故答案为:BF;
(2)BF=AC仍然成立,
理由:同(1)的方法直接得出,BF=AC,
(3)如图2, 过点B,C,D作圆交CF于G,连接BG,过点B作BM⊥CF,
过点B,C,D作圆交CF于G,连接BG,过点B作BM⊥CF,
∴∠BMF=90°,
∵点C,B,D,G四点共圆,
∵∠BEC+∠BDC=180°,∠BEC+∠BEF=180°,
∴∠BDC=∠BEF,
∵∠BGC=∠BDC,
∴∠BGE=∠BEG,
∴BG=BE,
∴∠BDC=∠BGC,
∵∠BEC+∠BDC=180°,
∴∠BEC+∠BGC=180°,
∵∠BGF+∠BGC=180°,
∴∠BGF=∠BEC,
∵∠FBG=∠DCF,
∴△BFG∽△CAE,
∴$\frac{FG}{AE}$=$\frac{BG}{CE}$,
∵BG=BE,
∴$\frac{FG}{AE}$=$\frac{BE}{CE}$,
∵CE=kBE,
∴$\frac{FG}{AE}$=$\frac{BE}{CE}$=$\frac{1}{k}$,
∴AE=kFG,
在Rt△BMF中,BF=m,∠BFE=α,
∴cosα=$\frac{FM}{BF}$,
∴FM=BF•cosα=m•cosα,
∵EF=n,
∴EF=FM+ME,
∴ME=EF-FM=n-m•cosα,
∵BG=BE,BM⊥CF,
∴EG=2ME=2(n-m•cosα),
∴FG=EF-EG=n-2(n-m•cosα),
∴AE=kFG=k[n-2(n-m•cosα)]=k(2m•cosα-n).
点评 此题是相似形综合题,主要考查了全等三角形的判定和性质,圆周角的性质,相似三角形性质和判定,锐角三角函数,等腰三角形的性质,作出辅助线是解本题的关键,用类比的方法得出后面两问是解本题的难点.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 1 | B. | -1 | C. | 0 | D. | 1或-1 |
 八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.
八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm. 如图,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于点D,在BC上取一点E,使得∠BAD=∠CAE,在AE上存在一点K,使得∠KBC=2∠BQD,求证:QK平分∠BKC.
如图,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于点D,在BC上取一点E,使得∠BAD=∠CAE,在AE上存在一点K,使得∠KBC=2∠BQD,求证:QK平分∠BKC. 如图,在等腰三角形ABC中,两腰上的中线BE、CD相交于点O.求证:OB=OC.
如图,在等腰三角形ABC中,两腰上的中线BE、CD相交于点O.求证:OB=OC. 已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.
已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.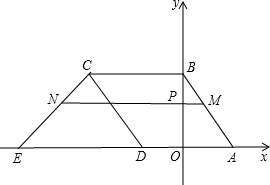 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.