题目内容
9. 已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.
已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.
分析 根据三角形的内角和以及平角的定义,证得∠DAB=∠EDC,则易证△ABD∽△DCE,根据相似三角形的性质,相似三角形的对应边的比相等即可求解.
解答  解:∵△ABC为等边三角形,AB=6cm,$\frac{DB}{DC}$=$\frac{1}{2}$,
解:∵△ABC为等边三角形,AB=6cm,$\frac{DB}{DC}$=$\frac{1}{2}$,
∴BD=2,CD=4,
∵∠ADE=∠B=60°,
∴∠BAD+∠BDA=120°=∠CDE+∠BDA,
∴∠BAD=∠CDE,
又∵∠B=∠C,
∴△ABD∽△DCE,
∴$\frac{CE}{BD}$=$\frac{CD}{BA}$,即$\frac{CE}{2}$=$\frac{4}{6}$,
解得CE=$\frac{4}{3}$,
∴AE=AC-CE=6-$\frac{4}{3}$=$\frac{14}{3}$cm.
点评 本题考查了相似三角形的判定与性质,利用相似三角形的性质列出比例式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
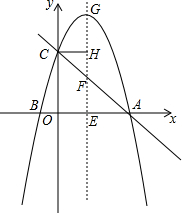 已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.
已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.
 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)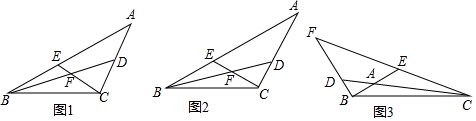
 在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).