题目内容
13.解一元一次不等式(组),并把解集表示在数轴上.(1)$\frac{2x-1}{3}≤x-\frac{x+1}{2}$
(2)$\left\{\begin{array}{l}{\frac{1}{3}x>\frac{1}{2}x}\\{3-5x≤8}\end{array}\right.$.
分析 (1)先去分母,再去括号,移项,合并同类项,并在数轴上表示出来即可;
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)去分母得,2(2x-1)≤6x-3(x+1),
去括号得,4x-2≤6x-3x-3,
移项得,4x-6x+3x≤-3+2,
合并同类项得,x≤-1.
在数轴上表示为: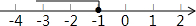 ;
;
(2)$\left\{\begin{array}{l}\frac{1}{3}x>\frac{1}{2}x①\\ 3-5x≤8②\end{array}\right.$,由①得,x<0,由②得,x≥-1.
故不等式组得解集为:-1≤x<0.
在数轴上表示为: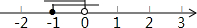 .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.给出的六个关系式:①x(y+1)②$y=\frac{2}{x+2}$③$y=\frac{1}{x^2}$④$y=-\frac{1}{2x}$⑤$y=\frac{x}{2}$⑥$y=\frac{2}{3x}$;其中y是x的反比例函数是( )
| A. | ①②③④⑥ | B. | ③⑤⑥ | C. | ①②④ | D. | ④⑥ |
12.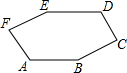 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )| A. | 160° | B. | 150° | C. | 145° | D. | 140° |
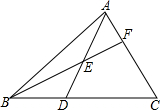 如图,在△ABC中,D为BC边上一点,E为线段AD上一点,延长BE交AC于点F.若$\frac{BD}{BC}=\frac{2}{5}$,$\frac{AE}{AD}=\frac{1}{2}$,则$\frac{AF}{AC}$=$\frac{2}{7}$.
如图,在△ABC中,D为BC边上一点,E为线段AD上一点,延长BE交AC于点F.若$\frac{BD}{BC}=\frac{2}{5}$,$\frac{AE}{AD}=\frac{1}{2}$,则$\frac{AF}{AC}$=$\frac{2}{7}$.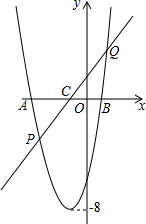 如图,已知二次函数的最小值是-8,它的图象与x轴交于A(-3,0)、B(1,0)两点,一次函数y=kx+b(k>0)的图象过点C(-1,0),且与该二次函数的图象交于P、Q两点.
如图,已知二次函数的最小值是-8,它的图象与x轴交于A(-3,0)、B(1,0)两点,一次函数y=kx+b(k>0)的图象过点C(-1,0),且与该二次函数的图象交于P、Q两点.