题目内容
12.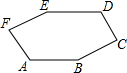 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )| A. | 160° | B. | 150° | C. | 145° | D. | 140° |
分析 首先延长DC、AB交于G,由AB∥ED,∠D=130°,根据两直线平行,同旁内角互补,即可求得∠G的度数,又由∠BCD=90°,∠BCD=∠G+∠CBG,即可求得∠CBG的度数,继而求得∠E的大小.
解答 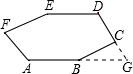 解:延长DC、AB交于G,
解:延长DC、AB交于G,
∵ED∥AB,∠D=130°,
∴∠G=50°,
又∵∠BCD=90°,∠BCD=∠G+∠CBG,
∴∠CBG=40°,
∴∠ABC=140°,
∴∠E=∠ABC=140°.
故选D.
点评 此题考查了平行线的性质与三角形外角的性质.此题难度不大,解题的关键是掌握两直线平行,同旁内角互补定理的应用与辅助线的作法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列方程为一元二次方程的是( )
| A. | x2=-2 | B. | (x+2)2=x(x-1) | C. | $\frac{1}{{x}^{2}}$$+\frac{2}{x}$=1 | D. | x2-2x+y=0 |
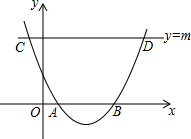 如图所示的抛物线与x轴交于A、B两点,与直线y=m交于C、D两点,请仅用没有刻度的直尺作出该抛物线的对称轴l.(保留作图痕迹,不写作法)
如图所示的抛物线与x轴交于A、B两点,与直线y=m交于C、D两点,请仅用没有刻度的直尺作出该抛物线的对称轴l.(保留作图痕迹,不写作法)