题目内容
5.已知函数y=(k+3)x.(1)k为何值时,函数为正比例函数;
(2)k为何值时,函数的图象经过一,三象限;
(3)k为何值时,y随x的增大而减小?
(4)k为何值时,函数图象经过点(1,1)?
分析 (1)根据正比例函数的定义得k+3≠0,然后解不等式即可;
(2)根据正比例函数的性质得k+3>0,然后解不等式即可;
(3)根据正比例函数的性质得k+3<0,然后解不等式即可;
(4)利用一次函数图象上点的坐标特征,把(1,1)代入y=(k+3)x中可求出k的值.
解答 解:(1)根据题意得k+3≠0,解得k≠-3;
(2)根据题意得k+3>0,解得k>-3;
(3)根据题意得k+3<0,解得k<-3;
(4)把(1,1)代入y=(k+3)x得k+3=1,解得k=-2,
即k为-2时,函数图象经过点(1,1).
点评 本考查了正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.也考查了一次函数的性质.

练习册系列答案
相关题目
4.下列方程为一元二次方程的是( )
| A. | x2=-2 | B. | (x+2)2=x(x-1) | C. | $\frac{1}{{x}^{2}}$$+\frac{2}{x}$=1 | D. | x2-2x+y=0 |
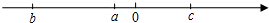 已知有理数a、b、c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b+c|.
已知有理数a、b、c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b+c|.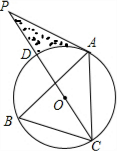 如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.