题目内容
4. 如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.(1)求BP的长;
(2)求图中阴影部分的面积(结果保留π).
分析 (1)如图,连接AP,通过解直角△ABP求得BP的长度;
(2)S阴影=S半圆O-(S扇形BOP-S△BOP).
解答 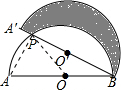 解:(1)如图,连接AP,
解:(1)如图,连接AP,
∵AB是圆O的直径,
∴∠APB=90°,
又由旋转的性质得到∠ABP=30°,
∴BP=AB•cos30°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$;
(2)如图,连接OP.
∵AB=20,∠ABP=30°,
∴OB=10,∠BOP=150°,
∴S阴影=S半圆O-(S扇形BOP-S△BOP)
=$\frac{1}{2}$π×202-($\frac{150π×1{0}^{2}}{360}$-$\frac{1}{2}$×10×10×sin150°)
=200π-($\frac{125π}{3}$-25)
=$\frac{475}{3}$π+25.
点评 本题考查了扇形面积的计算,旋转的性质,解题时,利用了锐角三角函数的概念,扇形的面积公式,三角形的面积公式,圆面积公式求解.

练习册系列答案
相关题目
8.若点A(2,3)在反比例函数y=$\frac{k}{x}$的图象上,则该图象一定经过点( )
| A. | (-2,3) | B. | (1,-6) | C. | (-3,-2) | D. | (3,3) |
14.下列实数中,最小的是( )
| A. | -1 | B. | -2 | C. | -$\sqrt{2}$ | D. | -$\frac{4}{3}$ |
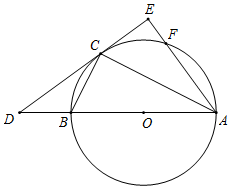 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{CF}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{CF}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.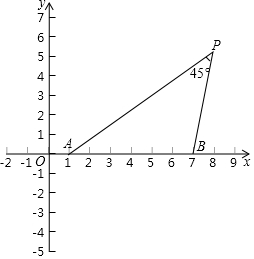 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0). 如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.
如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.