题目内容
16.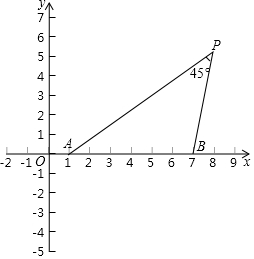 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).(1)对于坐标平面内的一点P,给出如下定义:如果∠APB=45°,则称点P为线段AB的“等角点”.显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
①设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和⊙C的半径;
②y轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
(2)当点P在y轴正半轴上运动时,∠APB是否有最大值?如果有,说明此时∠APB最大的理由,并求出点P的坐标;如果没有请说明理由.
分析 (1)①如图1中,在x轴的上方,作以AB为斜边的直角三角形△ACB,易知A、B、P三点在⊙C上,点C即为所求,再根据对称性可知满足条件的所有点C坐标.
②y轴的正半轴上存在线段AB的“等角点“.如图2所示:当圆心为C(4,3)时,过点C作CD⊥y轴于D,则D(0,3),CD=4,设交点为P1、P2,此时P1、P2在y轴的正半轴上连接CP1、CP2、CA,则CP1=CP2=CA=r=$3\sqrt{2}$Y2CD⊥y轴,CD=4,CP1=$3\sqrt{2}$,推出DP1=$\sqrt{CP_1^2-C{D^2}}=\sqrt{2}$=DP2,由此即可解决问题;
(2)当过点A,B的圆与y轴正半轴相切于点P时,∠APB最大.
解答 解:(1)①如图1中,
在x轴的上方,作以AB为斜边的直角三角形△ACB,易知A、B、P三点在⊙C上,
圆心C的坐标为(4,3),半径为3$\sqrt{2}$,
根据对称性可知点C(4,-3)也满足条件.
②y轴的正半轴上存在线段AB的“等角点“.
如图2所示:当圆心为C(4,3)时,过点C作CD⊥y轴于D,则D(0,3),CD=4
∵⊙C的半径r=$3\sqrt{2}$>4,
∴⊙C与y轴相交,
设交点为P1、P2,此时P1、P2在y轴的正半轴上
连接CP1、CP2、CA,则CP1=CP2=CA=r=$3\sqrt{2}$
∵CD⊥y轴,CD=4,CP1=$3\sqrt{2}$,
∴DP1=$\sqrt{CP_1^2-C{D^2}}=\sqrt{2}$=DP2,
∴P1(0,3+$\sqrt{2}$) P2(0,3-$\sqrt{2}$).
(2)当过点A,B的圆与y轴正半轴相切于点P时,∠APB最大.
理由如下:如果点P在y轴的正半轴上,设此时圆心为E,则E在第一象限,
在y轴的正半轴上任取一点M(不与点P重合),
连接MA,MB,PA,PB,设MB交于⊙E于点N,连接NA,
∵点P,点N在⊙E上,∴∠APB=∠ANB,
∵∠ANB是△MAN的外角,
∴∠ANB>∠AMB,即∠APB>∠AMB,
此时,过点E作EF⊥x轴于F,连接EA,EP,则AF=$\frac{1}{2}$AB=3,OF=4,
∵⊙E与y轴相切于点P,则EP⊥y轴,
∴四边形OPEF是矩形,OP=EF,PE=OF=4.
∴⊙E的半径为4,即EA=4,
∴在Rt△AEF中,EF=$\sqrt{E{A^2}-A{F^2}}=\sqrt{{4^2}-{3^3}}=\sqrt{7}$,
∴OP=$\sqrt{7}$即 P(0,$\sqrt{7}$).
点评 本题考查圆综合题、圆周角定理、直线与圆位置关系、勾股定理、线段AB的“等角点”的定义等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,所有中考压轴题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 下面立体图形的左视图为( )
下面立体图形的左视图为( )| A. |  | B. |  | C. |  | D. |  |
| A. | 9608×102 | B. | 960.8×103 | C. | 96.08×104 | D. | 9.608×105 |
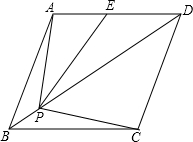 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.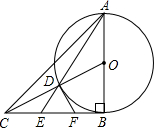 如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.
如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.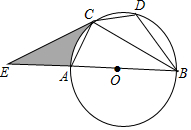 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.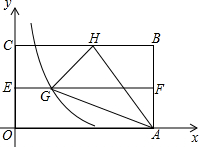 如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.
如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.