题目内容
13.观察下列二次根式的化简:S1=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$
S2=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=(1+$\frac{1}{1}$-$\frac{1}{2}$)+(1+$\frac{1}{2}$-$\frac{1}{3}$)
S3=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=(1+$\frac{1}{1}$-$\frac{1}{2}$)(1+$\frac{1}{2}$-$\frac{1}{3}$)+(1+$\frac{1}{3}$-$\frac{1}{4}$),….
则$\frac{{S}_{2017}}{2017}$=$\frac{2019}{2017}$.
分析 根据题意可归纳出Sn的表达式,从而求出S2017的值
解答 解:由题意可知:S1=1+$\frac{1}{1}$-$\frac{1}{2}$=2-$\frac{1}{2}$
S2=1+1+$\frac{1}{1}$-$\frac{1}{3}$=3-$\frac{1}{3}$
S3=1+1+1+$\frac{1}{1}$-$\frac{1}{4}$=4-$\frac{1}{4}$
由此可知:Sn=(n+1)-$\frac{1}{n+1}$=$\frac{n(n+2)}{n+1}$
∴$\frac{{S}_{n}}{n}$=$\frac{n+2}{n+1}$=$\frac{2019}{2017}$
点评 本题考查数字规律问题,解题的关键是根据题意求出Sn的表达式,本题属于中等题型.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
1.五一假期,黄石市退出了东方山休闲娱乐、传统文化展演、游园赏景赏花、佛教文化体验等精品文化活动,共接待旅游总人数9 608 00人次,将9 608 00用科学记数法表示为( )
| A. | 9608×102 | B. | 960.8×103 | C. | 96.08×104 | D. | 9.608×105 |
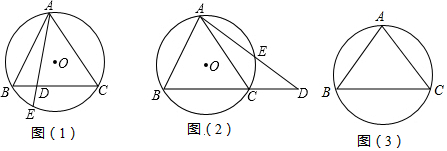
 如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺时针旋转30°得到半圆O′,与AB交于点P.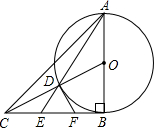 如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.
如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.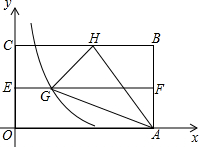 如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.
如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.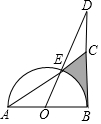 如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.
如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.