题目内容
17.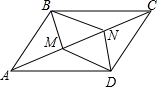 已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.
已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.
分析 先证明△ABM≌△CDN,再证明BM=DN,BM∥DN即可.
解答  证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AB=CD,AB∥DC,
∵BM平分∠ABC,DN平分∠ADC,
∴∠ABM=$\frac{1}{2}$∠ABC,∠CDN=$\frac{1}{2}$∠ADC,
∴∠ABM=∠CDN,∠BAM=∠DCN,
在△ABM和△CDN中,
$\left\{\begin{array}{l}{∠ABM=∠CDN}\\{AB=CD}\\{∠BAM=∠DCN}\end{array}\right.$,
∴△ABM≌△CDN,
∴BM=DN,∠AMB=∠CND,
∵∠BMN=180°-∠AMB,∠DNM=180°-∠CND,
∴∠BMN=∠MND,
∴BM∥DN,
∴四边形BMDN是平行四边形.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识,熟练掌握全等三角形的判定和性质是解决问题的关键,属于中考常考题型.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).
如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).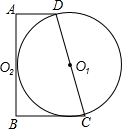 如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.
如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.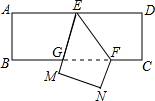 如图所示,把一张长方形纸片ABCD沿EF折叠,若∠AEG=60°,则∠EFG的度数是60°,则∠GFN度数是60°.
如图所示,把一张长方形纸片ABCD沿EF折叠,若∠AEG=60°,则∠EFG的度数是60°,则∠GFN度数是60°.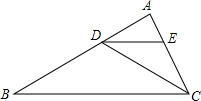 如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由.
如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由.