题目内容
7.先化简,再求值:$\frac{1}{2ab}$-$\frac{1}{a-b}$($\frac{a-b}{2ab}$+$\frac{-{a}^{2}+{b}^{2}}{2ab}$),其中a=$\frac{1}{2}$(3-2$\sqrt{2}$),b=$\frac{1}{2}$(3+2$\sqrt{2}$).分析 将原分式按照提取公因式、合并同类项的方法进行化简,再将a、b的值代入化简后的代数式中即可得出结论.
解答 解:原式=$\frac{1}{2ab}$-$\frac{1}{a-b}$•$\frac{(b-a)(b+a-1)}{2ab}$,
=$\frac{1}{2ab}$+$\frac{a+b-1}{2ab}$,
=$\frac{a+b}{2ab}$.
当a=$\frac{1}{2}$(3-2$\sqrt{2}$),b=$\frac{1}{2}$(3+2$\sqrt{2}$)时,
原式=$\frac{a+b}{2ab}$=$\frac{\frac{1}{2}(3-2\sqrt{2}+3+2\sqrt{2})}{2×\frac{1}{4}(3-2\sqrt{2})(3+2\sqrt{2})}$=6.
点评 本题考查了分式的化简求值,解题的关键是将原分式进行化简.本题属于基础题,难度不大,解决该题型题目时,按照化简分式的方法将原式进行化简,化简后再代入数据求值.

练习册系列答案
相关题目
11.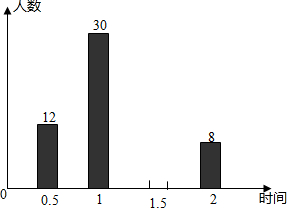 某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
(1)统计表中的m=100,x=50,y=0.08;
(2)被抽样调查的同学劳动时间的众数是1.5,中位数是1.5;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
 某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.5 |
| 2 | 8 | y |
| 合计 | m | 1 |
(2)被抽样调查的同学劳动时间的众数是1.5,中位数是1.5;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
12.要使二次根式$\sqrt{5-2x}$有意义,则x的取值范围是( )
| A. | x$>\frac{5}{2}$ | B. | x$≥\frac{2}{5}$ | C. | x$≤\frac{5}{2}$ | D. | x$≤\frac{2}{5}$ |
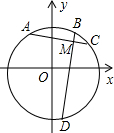 半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.
半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.
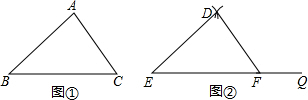
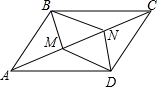 已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.
已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.