题目内容
9.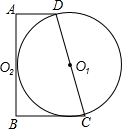 如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.
如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.
分析 首先证得O2是⊙O1的切点,然后过点O2作O2F⊥CD于点F,易证得△AO2D≌△FO2D,即可得O2F=O2A=$\frac{1}{2}$AB,则可判定CD与⊙O2相切.
解答 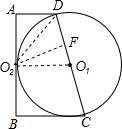 证明:,设AB与⊙O1的切点为E,连接OE,
证明:,设AB与⊙O1的切点为E,连接OE,
∴OE⊥AB,
∵DA⊥AB,BC⊥AB,
∴AD∥O1E∥BC,
∵O1D=O1C
∴O1E是梯形ABCD的中位线,
∴E是AB的中点,
∴E与O2重合,
∴O1O2=O1D,
∴∠O1O2D=∠O1DO2,
∵AD∥O1O2,
∴∠ADO2=∠DO2O1=∠O2DO1,
过点O2作O2F⊥CD于点F,
在△AO2D和△FO2D中,
$\left\{\begin{array}{l}{∠DA{O}_{2}=∠{O}_{2}FD=90°}\\{∠AD{O}_{2}=∠{O}_{2}DF}\\{{O}_{2}D={O}_{2}D}\end{array}\right.$,
∴△AO2D≌△FO2D(AAS),
∴O2F=O2A=$\frac{1}{2}$AB,
即CD与⊙O2相切.
点评 本题考查了切线的判定和性质,三角形全等的判定和性质,证得O2是⊙O1的切点是解题的关键.

练习册系列答案
相关题目
19.一个正数的算术根为m,则比这个数大2的数的算术平方根是( )
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.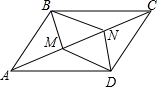 已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.
已知:如图,在?ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N.求证:四边形BMDN是平行四边形.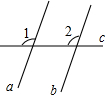 同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)
同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)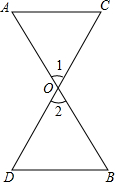 如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么?
如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么? 如图所示,已知直线a,b,c,d,e,b∥c,且∠1=∠2,a与c平行吗?说明理由.
如图所示,已知直线a,b,c,d,e,b∥c,且∠1=∠2,a与c平行吗?说明理由.