题目内容
7．
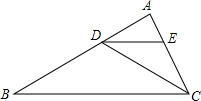如图，已知∠ABC=30°，∠ADC=60°，DE为∠ADC的平分线，你能判断哪两条直线平行吗，并说明理由．
分析 根据角平分线的性质以及同位角相等两直线平行得出即可．
解答 解：BC∥DE，
理由如下：
∵DE为∠ADC的平分线，∠ADC=60°，
∴∠ADE=∠EDC=30°，
∵∠ABC=30°，
∴∠ADE=∠ABC，
∴BC∥DE
点评 此题主要考查了角平分线的性质以及平行线的判定，熟练掌握平行线的判定是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
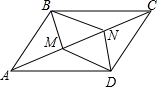已知：如图，在?ABCD中，∠ABC、∠ADC的平分线分别交对角线AC于点M、N．求证：四边形BMDN是平行四边形．
如图所示，已知直线a，b，c，d，e，b∥c，且∠1=∠2，a与c平行吗？说明理由．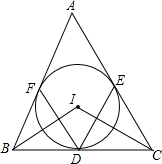
如图，△ABC中，内切圆I和边BC，CA，AB分别相切于点D，F，求证：
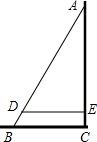如图，AB是斜靠在墙上的长梯，梯脚B距墙脚1.6m，梯上点D距墙1.4m，BD长0.55m，求该梯子的长．
19．一个正数的算术根为m，则比这个数大2的数的算术平方根是（ ）
| A． | $\sqrt{{m}^{2}+2}$ | B． | $\sqrt{m+2}$ | C． | m2+2 | D． | m+2 |
16．
如图，用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为（ ）
如图，用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为（ ）| A． | $（{\sqrt{2}-1}）a$ | B． | $\frac{{\sqrt{2}-1}}{2}a$ | C． | $\frac{{2-\sqrt{2}}}{4}a$ | D． | $（{2-\sqrt{2}}）a$ |
