题目内容
11.在长株潭建设两型社会的过程中,为推进节能减排,发展低碳经济,我市某公司以25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工.已知生产这种产品的成本价为每件20元.经过市场调研发现,该产品的销售单价定在25元到30元之间较为合理,并且该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为:y=$\left\{\begin{array}{l}{40-x(25≤x≤30)}\\{25-0.5x(30<x≤35)}\end{array}\right.$(年获利=年销售收入-生产成本-投资成本)(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3)第二年,该公司决定给希望工程捐款Z万元,该项捐款由两部分组成:一部分为10万元的固定捐款;另一部分则为每销售一件产品,就抽出一元钱作为捐款.若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,到第二年年底,两年的总盈利不低于67.5万元,请你确定此时销售单价的范围.
分析 (1)因为25<28<30,所以把x=28代入y=40-x即可求出该产品的年销售量为多少万件;
(2)由(1)中y与x的函数关系式和根据年获利=年销售收入-生产成本-投资成本,得到w和x的二次函数关系,再由x的取值范围不同分别讨论即可知道该公司是盈利还是亏损,若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3)由题目的条件得到w和x在自变量x的不同取值范围的函数关系式,再分别当w≥67.5,求出对应x的范围,结合y于x的关系中的x取值范围即可确定此时销售单价的范围.
解答 解:(1)∵25≤28≤30,y=$\left\{\begin{array}{l}{40-x}&{25≤x≤30}\\{25-0.5x}&{30<x≤35}\end{array}\right.$,
∴把x=28代入y=40-x得,
∴y=12(万件),
答:当销售单价定为28元时,该产品的年销售量为12万件;
(2)①当 25≤x≤30时,W=(40-x)(x-20)-25-100=-x2+60x-925=-(x-30)2-25,
故当x=30时,W最大为-25,即公司最少亏损25万;
②当30<x≤35时,W=(25-0.5x)(x-20)-25-100
=-$\frac{1}{2}$x2+35x-625=-$\frac{1}{2}$(x-35)2-12.5
故当x=35时,W最大为-12.5,即公司最少亏损12.5万;
对比①,②得,投资的第一年,公司亏损,最少亏损是12.5万;
答:投资的第一年,公司亏损,最少亏损是12.5万;
(3)①当 25≤x≤30时,W=(40-x)(x-20-1)-12.5-10=-x2+61x-862.5≥67.5,
-x2+61x-862.5≥67.5,
化简得:x2-61x+930≤0
解得:30≤x≤31,
当两年的总盈利不低于67.5万元时,x=30;
②当30<x≤35时,W=(25-0.5x)(x-20-1)-12.5-10=-$\frac{1}{2}$x2+35.5x-547.5≥67.5,
化简得:x2-71x+1230≤0
解得:30≤x≤41,
当两年的总盈利不低于67.5万元时,30<x≤35,
答:到第二年年底,两年的总盈利不低于67.5万元,此时销售单价的范围是30≤x≤35.
点评 本题主要考查二次函数的实际应用能力及二次函数与一元二次不等式间关系,理解题意准确抓住相等关系是解题的关键,结合题意分类去求是解题的难点.

| 甲 | 7 | 9 | 8 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 7 | 8 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
| A. | 5×109米 | B. | 50×10-8米 | C. | 5×10-9米 | D. | 5×10-8米 |
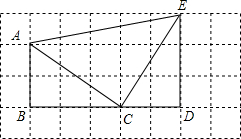 如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.