题目内容
2.公园路中学组织了一次教师踢毽子比赛,甲、乙两教研组每队各10人的比赛成绩如表(10分制):| 甲 | 7 | 9 | 8 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 7 | 8 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
分析 (1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
解答 解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
(2)乙队的平均成绩是:$\frac{1}{10}$×(10×4+8×2+7+9×3)=9,
则方差是:$\frac{1}{10}$×[4×(10-9)2+2×(8-9)2+(7-9)2+3×(9-9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队.
故答案为:(1)9.5 10 (3)乙
点评 本题考查方差、中位数、众数、平均数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);一组数据中出现次数最多的数据叫做众数;平均数是所有数据的和除以数据的个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.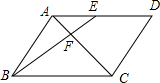 如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
 如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )| A. | 1:4 | B. | 1:2 | C. | 1:9 | D. | 4:1 |
14.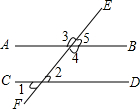 如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
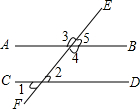 如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )| A. | 如果∠5=50°,那么AB∥CD | B. | 如果∠4=130°,那么AB∥CD | ||
| C. | 如果∠3=130°,那么AB∥CD | D. | 如果∠2=50°,那么AB∥CD |
12.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周零花钱的情况 | B. | 旅客上飞机前的安检 | ||
| C. | 工厂招聘工人,对应聘人员体检 | D. | 了解全国中小学生的身高情况 |
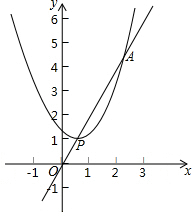 如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.
如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.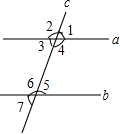 如图,直线a,b被直线c所截,现给出下列四个条件:
如图,直线a,b被直线c所截,现给出下列四个条件: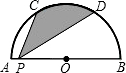 如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.