题目内容
1.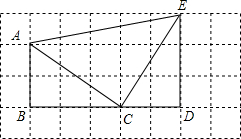 如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
分析 利用勾股定理表示出AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;CE=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;AE=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$;再利用勾股定理的逆定理得到三角形为直角三角形.
解答 解:△ACE是直角三角形.理由如下:
∵在△ACE中,
AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
CE=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
AE=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$;
∴AC2+CE2=AE2,
∴∠ACE=90°,△ACE是直角三角形,
点评 本题考查了勾股定理、勾股定理逆定理、三角形的面积,充分利用网格是解题的关键.

练习册系列答案
相关题目
12.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周零花钱的情况 | B. | 旅客上飞机前的安检 | ||
| C. | 工厂招聘工人,对应聘人员体检 | D. | 了解全国中小学生的身高情况 |
10.已知:|a|=3,$\sqrt{{b}^{2}}$=5,且|a+b|=a+b,则a-b的值为( )
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
11. 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )
 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )| A. | ∠1=∠4 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | ∠1=∠5 |
 如图所示,已知∠AOB=90°,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图所示,已知∠AOB=90°,∠BOC=40°,OD平分∠AOC,求∠BOD的度数. 如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16.
如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16. 如图,DE⊥BC于E,且BE=CE,AB+AC=15,则△ABD的周长是15.
如图,DE⊥BC于E,且BE=CE,AB+AC=15,则△ABD的周长是15.