题目内容
1.计算:(1)$\sqrt{8}+\sqrt{32}-\sqrt{2}$
(2)$(\sqrt{5}-2)(2+\sqrt{5})$$-{(-\sqrt{3})^2}+\sqrt{8}×\frac{1}{{\sqrt{2}}}$.
分析 (1)先对式子进行化简,再合并同类项即可解答本题;
(2)根据平方差公式对式子进行化简,然后再合并同类项即可解答本题.
解答 解:(1)$\sqrt{8}+\sqrt{32}-\sqrt{2}$
=$2\sqrt{2}+4\sqrt{2}-\sqrt{2}$
=5$\sqrt{2}$;
(2)$(\sqrt{5}-2)(2+\sqrt{5})$$-{(-\sqrt{3})^2}+\sqrt{8}×\frac{1}{{\sqrt{2}}}$
=$(\sqrt{5})^{2}-{2}^{2}-3+2\sqrt{2}×\frac{1}{\sqrt{2}}$
=5-4-3+2
=0.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.计算x3•x3的结果是( )
| A. | 2x3 | B. | 2x6 | C. | x6 | D. | x9 |
10.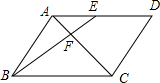 如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
 如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )| A. | 1:4 | B. | 1:2 | C. | 1:9 | D. | 4:1 |
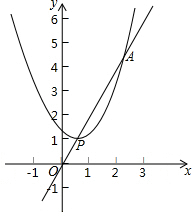 如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.
如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.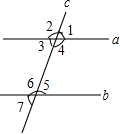 如图,直线a,b被直线c所截,现给出下列四个条件:
如图,直线a,b被直线c所截,现给出下列四个条件: