题目内容
13．
如图所示，已知∠1=∠2，∠B=60°，∠ACB=80°，求∠BCD的度数．
分析 根据三角形的内角和为180°，先求得∠A的度数，再利用△ACD中，∠1=∠2，求得∠1=∠2=70°，利用∠BCD=∠ACB-∠2即可解答．
解答 解：∵在△ABC中，∠B=60°，∠ACB=80°，
∴∠A=180°-∠B-∠ACB=180°-60°-80°=40°，
∵∠1=∠2，
∴∠1=∠2=（180°-∠A）÷2=（180°-40°）÷2=70°，
∴∠BCD=∠ACB-∠2=80°-70°=10°．
点评 本题考查了三角形的内角和，解决本题的关键是熟记三角形内角和为180度．
练习册系列答案
53天天练系列答案
相关题目
如图，已知直线a，b交于点O，∠1+∠2=218°，则∠1=109°，∠2=109°，∠3=71°．
1．已知y=2x，z=$\frac{1}{y}$，那么z与x之间的关系是（ ）
| A． | 成正比例 | B． | 成反比例 | ||
| C． | 有可能成正比例有可能成反比例 | D． | 无法确定 |
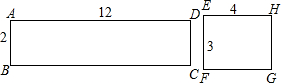
18．矩形ABCD中，AB=4，BC=$\sqrt{3}$，点E在AB上，EF∥BC，交CD于F，且矩形AEFD∽矩形EFCB，则AE等于（ ）
| A． | $\frac{3}{4}$ | B． | 1或2 | C． | 1或3 | D． | 2或3 |
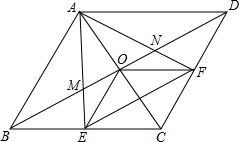如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）